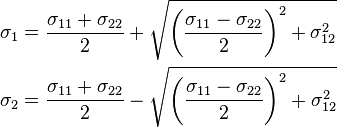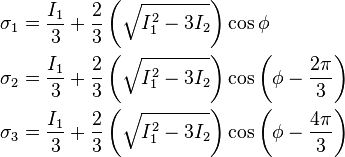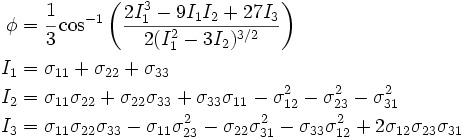Principal stresses

Principal Stresses in Two and Three Dimensions

The principal stresses are the components of the stress tensor when the basis is changed in such a way that the shear stress components become zero. To find the principal stresses in two dimensions, we have to find the angle 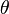$\textstyle \theta$ at which 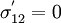$\textstyle \sigma^{'}_{12} = 0$ . This angle is given by

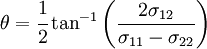
$\theta = \cfrac{1}{2}\tan^{-1}\left(\frac{2\sigma_{12}}{\sigma_{11}-\sigma_{22}}\right)$

Plugging 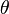$\textstyle \theta$ into the transformation equations for stress we get,

\begin{align} \sigma_1 &= \frac{\sigma_{11}+\sigma_{22}}{2} +\sqrt{\left(\frac{\sigma_{11}-\sigma_{22}}{2}\right)^2 + \sigma_{12}^2} \\ \sigma_2 &= \frac{\sigma_{11}+\sigma_{22}}{2} -\sqrt{\left(\frac{\sigma_{11}-\sigma_{22}}{2}\right)^2 + \sigma_{12}^2} \end{align}

Where are the shear tractions usually zero in a body?

The principal stresses in three dimensions are a bit more tedious to calculate. They are given by,

\begin{align} \sigma_1 & = \frac{I_1}{3} + \frac{2}{3} \left(\sqrt{I^2_1 - 3I_2}\right)\cos\phi \\ \sigma_2 & = \frac{I_1}{3} + \frac{2}{3} \left(\sqrt{I^2_1 - 3I_2}\right) \cos\left(\phi-\frac{2\pi}{3}\right) \\ \sigma_3 & = \frac{I_1}{3} + \frac{2}{3} \left(\sqrt{I^2_1 - 3I_2}\right) \cos\left(\phi-\frac{4\pi}{3}\right) \end{align}

where,

\begin{align} \phi & = \cfrac{1}{3}\cos^{-1}\left(\frac{2I_1^3 - 9I_1I_2 + 27 I_3}{2(I_1^2 - 3I_2)^{3/2}}\right) \\ I_1 & = \sigma_{11} + \sigma_{22} + \sigma_{33} \\ I_2 & = \sigma_{11}\sigma_{22} + \sigma_{22}\sigma_{33} + \sigma_{33}\sigma_{11} - \sigma_{12}^2 - \sigma_{23}^2 - \sigma_{31}^2 \\ I_3 & = \sigma_{11}\sigma_{22}\sigma_{33} - \sigma_{11}\sigma_{23}^2 - \sigma_{22}\sigma_{31}^2 - \sigma_{33}\sigma_{12}^2 + 2\sigma_{12}\sigma_{23}\sigma_{31} \end{align}

The quantities 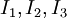$\textstyle I_1, I_2, I_3$ are the stress invariants.

Related Content

Introduction to Elasticity

This article is issued from Wikiversity - version of the Wednesday, December 30, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.