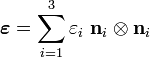Principal strains

The principal values (eigenvalues) 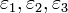\textstyle \varepsilon_1, \varepsilon_2, \varepsilon_3 of a strain tensor 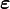\textstyle \boldsymbol{\varepsilon} are called the principal strains.

If the corresponding principal directions (eigenvectors) are 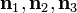\textstyle \mathbf{n}_1, \mathbf{n}_2, \mathbf{n}_3, then

\boldsymbol{\varepsilon} = \sum^3_{i=1} \varepsilon_i ~ \mathbf{n}_i\otimes\mathbf{n}_i

is called the spectral decomposition of 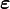\textstyle \boldsymbol{\varepsilon}.

Related Content

Introduction to Elasticity

This article is issued from Wikiversity - version of the Friday, August 03, 2007. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.