PlanetPhysics/Fundamental Theorem of Integral Calculus

< PlanetPhysics

Consider the sequence of numbers 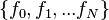$\{f_0,f_1,...f_N\}$ and define the difference 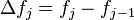$\Delta f_j = f_j-f_{j-1}$ . Now sum the differences and not that all but the first and last terms cancel:

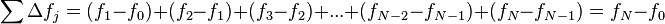
$\sum \Delta f_j = (f_1-f_0) + (f_2-f_1) + (f_3-f_2) + ... + (f_{N-2} - f_{N-1}) + (f_N - f_{N-1}) = f_N-f_0$

In other words 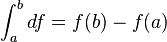$\int_a^bdf = f(b)-f(a)$ . It seems obvious that,

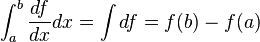
$\int_a^b\frac{df}{dx}dx= \int df = f(b)-f(a)$

Changing variables:

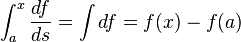
$\int_a^x\frac{df}{ds}= \int df = f(x)-f(a)$

or as an indefinite integral:

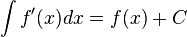
$\int f'(x)dx = f(x) + C$

Converse

In other words, the integral of the derivative of a function is the original function. But what of the derivative of the integral? Let,

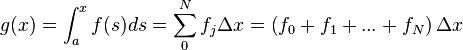$g(x) = \int_a^x f(s)ds = \sum_0^N f_j \Delta x = \left(f_0+f_1+...+f_N \right)\Delta x$ where $f_N = f(x)$ .

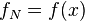Here, we assume that all the intervals 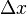$\Delta x$ in the Riemann sum are equal. To find 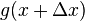$g(x+\Delta x)$ we need to add one extra term to the Riemann sum:

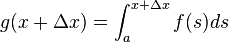
$g(x+\Delta x) = \int_a^{x+\Delta x} f(s)ds$

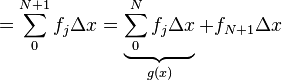= \sum_0^{N+1} f_j \Delta x = \underbrace{\sum_0^{N} f_j \Delta x}_{g(x)} + f_{N+1}\Delta x

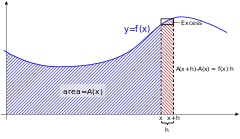
As shown in red, the change in area (∫fdx) of a function is closely related to the value of the function, f(x) at the point where x changes to x+δx

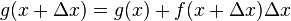$g(x+\Delta x) = g(x) + f(x+\Delta x)\Delta x$ .

Rearrange this to obtain:

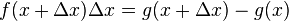
$f(x+\Delta x)\Delta x = g(x+\Delta x) - g(x)$

The original Planet Physics version still remains on the page as a hidden comment (visible in "edit" mode)

This article is issued from Wikiversity - version of the Wednesday, February 24, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.