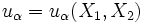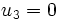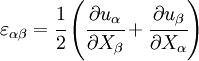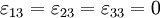Plane strain

A displacement field 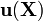\textstyle \mathbf{u}(\mathbf{X}) is called plane if

u_\alpha = u_\alpha(X_1, X_2) \,

and

u_3 = 0 \,

The corresponding strain field is called a plane strain and satisfies

\varepsilon_{\alpha\beta} = \cfrac{1}{2}\left(\cfrac{\partial{u_\alpha}}{\partial X_\beta}+ \cfrac{\partial{u_\beta}}{\partial X_\alpha}\right)

and

\varepsilon_{13}= \varepsilon_{23}= \varepsilon_{33}=0

This happens where one dimension is very large compared to the others, the principal strain in the direction of the longest dimension is constrained and can be assumed as zero, yielding a plane strain condition.

Related Content

Introduction to Elasticity

This article is issued from Wikiversity - version of the Saturday, March 12, 2011. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.