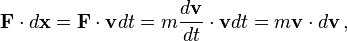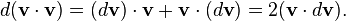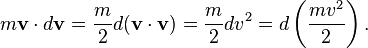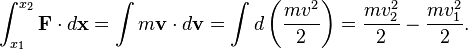Physics equations/Work, energy, power

Define kinetic energy, work, and potential energy

Symbols used for kinetic energy include KE (or K.E.), T, and K . Using the latter, we have for kinetic energy:

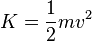
$K =\frac{1}{2}mv^2\;$

In shorthand-to-powerful notation, we can write these expressions for work:

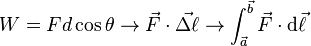
$W = F d\cos\theta\rightarrow\vec F\cdot\vec{\Delta\ell}\rightarrow\int_\vec a^\vec b \vec F\cdot\rm d\vec\ell$

Potential energy can be defined for conservative forces. Two important conservative forces are gravity and that of an ideal spring. Symbols for potential energy include PE (or PE) and V, and U:

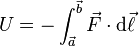
$U = -\int_\vec a^\vec b \vec F\cdot\rm d\vec\ell$

At Earth's surface, the gravitational P.E. is U_g = mgy, where g = 9.8 m/s² ("standard gravity"). and for a spring, U = ½kx², where x is the displacement from the spring's equilibrium position. The total mechanical energy (often written as M.E. or just E) is conserved if all forces are conservative: E_i = K_i+U_i = K_f+U_f=E_f Mechanical energy is not conserved if non-conservative forces are present. Friction is an important non-conservative force. Energy conservation can be stated as:

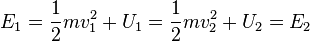
$E_1 = \frac{1}{2}mv_1^2 + U_1 = \frac{1}{2}mv_2^2 + U_2 = E_2\,$

*Problem: Describe a conservative and a nonconservative force in sports.

- click to show or hide solution -

Solution:

The pitcher throwing the ball is an example of work, by a nonconservative force. When a baseball player uses his or her arm to slow the moving ball to a stop, there is no storage of energy. The archer's bow does store energy, that can be converted back to kinetic energy (although in reality, the bow will receive less than 100% of the energy put into the bow by the archer.

****Problem: Use calculus to show why these equations are true

- click to show or hide solution -

Solution: The work done accelerating a particle during the infinitesimal time interval dt is given by the dot product of force and displacement:

\mathbf{F} \cdot d \mathbf{x} = \mathbf{F} \cdot \mathbf{v} d t = m\frac{d \mathbf{v}}{d t} \cdot \mathbf{v} d t = m\mathbf{v} \cdot d \mathbf{v}\,,

Applying the product rule we see that:

d(\mathbf{v} \cdot \mathbf{v}) = (d \mathbf{v}) \cdot \mathbf{v} + \mathbf{v} \cdot (d \mathbf{v}) = 2(\mathbf{v} \cdot d\mathbf{v}).

Therefore (assuming constant mass so that dm=0), the following can be seen:

m \mathbf{v} \cdot d \mathbf{v} = \frac{m}{2} d (\mathbf{v} \cdot \mathbf{v}) = \frac{m}{2} d v^2 = d \left(\frac{m v^2}{2}\right).

Since this is a total differential (that is, it only depends on the final state, not how the particle got there), we can integrate it and call the result kinetic energy:

\int_{x_1}^{x_2} \mathbf{F} \cdot d \mathbf{x} = \int m\mathbf{v} \cdot d \mathbf{v} = \int d \left(\frac{m v^2}{2}\right) = \frac{m v_2^2}{2}-\frac{m v_1^2}{2}.

Thus the change in kinetic energy equals the integral of the net force over distance.^[1]

↑ https://en.wikiversity.org/w/index.php?title=Advanced_Classical_Mechanics/Energy_and_Angular_Momentum&oldid=573819

*Problem: Energy conservation with a mass, a spring, and a hill

E=KE+PE

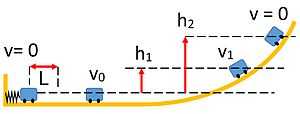
A spring with spring constant, k, is compressed by a distance x₀. A mass, m, is placed on the spring and it is released, sliding initially along a horizontal surface at a speed of v₁. Sliding without friction, it encounters a hill where it rises to a height, h₂ as it continues to move at a speed of v₂. Finally it reaches a height of h₃, where it stops. Write equations to model the particle's speed and height at each stage.

- click to show or hide solution -

Solution: ½kL² = ½mv₀² = ½mv₁² + mgh₁ = mgh₂

Power

Power, P, is the rate at which work is done or energy is consumed. The SI unit of power is Watt (W) which equals one Joule per second (J/s).

**Problem: Show that power is the dot product of force and velocity

- click to show or hide solution -

Solution: This solution was extracted from Physics with Calculus (Wikibook) and uses the notation of that chapter:

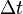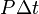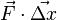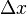Power is the rate of doing work. To come up with a useful expression for this, consider a short amount of time $\Delta t$ . How much work is done in that time? Well, by the definition of power, it is very nearly $P \Delta t$ . By the definition of work, this is $\vec{F} \cdot \vec{\Delta x}$ where $\Delta x$ is the displacement which occurs in 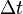$\Delta t$ . We have

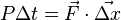
$P \Delta t = \vec{F} \cdot \vec{\Delta x}$

So,

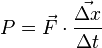$P = \vec{F} \cdot \frac{\vec{\Delta x}}{\Delta t}$ ,

which in the limit as 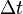$\Delta t$ goes to zero (which is when our "equations" become exact),

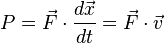$P = \vec{F} \cdot \frac{d\vec{x}}{dt} = \vec{F} \cdot \vec{v}$ .

Equivalently, we could have gotten the expression by simply differentiating our expression for work. No matter the derivation, because it simply does not matter that much; we have a useful expression for power.

This article is issued from Wikiversity - version of the Sunday, June 22, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.