Physics equations/Static forces
< Physics equationsMost applications of Newton's laws require only a few equations

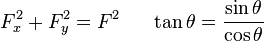
Friction and the normal force
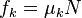 is the force friction when an object is sliding on a surface, where μk ("mew-sub-k") is the kinetic coefficient of friction, and N is the normal force.
is the force friction when an object is sliding on a surface, where μk ("mew-sub-k") is the kinetic coefficient of friction, and N is the normal force.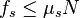 establishes the maximum possible friction (called static friction) that can occur before the object begins to slide. Usually μs > μk.
establishes the maximum possible friction (called static friction) that can occur before the object begins to slide. Usually μs > μk.
Also, air drag often depends on speed, an effect this model fails to capture. These equations for static and kinetic friction almost always are valid only as approximations.
*** Problem: Generating equations from adding forces
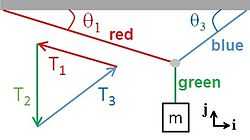 Three forces of tension are acting on the small grey circle at the center. |
Find the x and y components of the three forces on the small grey circle at the center - click to see or hide solution - Solution:
|
*** Problem: Almost proving Netwon's third law (one dimensional)
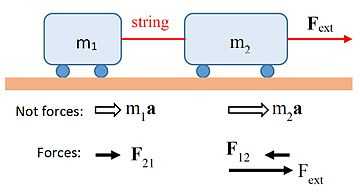 Two carts are connected by a string; a force is applied to one. By Newton's third law, the force on 1 by 2 equals the force on 2 by t. But we do not need Newton's third law to solve this problem. |
Consider two carts of mass known masses (m1 and m2) connected by a taught string, with one mass (m2) experiencing and external force of known magnitude. Assume that the collection of objects held together by a taught string obeys F=(m1+m2)a where F is the sum of all external forces. But we do not assume that string (in the middle) exerts equal and opposite forces on the two objects. (In this way we prove Newton's third law.) - click to see or hide solution - Solution: We take the acceleration, as well as the two internal forces as unknowns (we have three unknowns because we make no assumption about the equality of the two internal forces transmitted by the string, which we assume to have negligible mass. With three unknowns, we seek three equations. Beginning with Newton's second law (ΣF=ma) applied to and M=m1+m2, we have:
(They all have the same acceleration because the string is assumed taught.)
|
*** Problem: A free-body diagram on a system with many parts
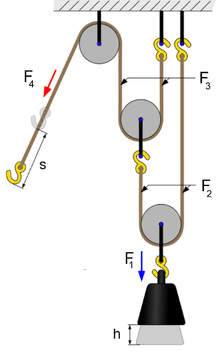 Power Pulley |
Make free body diagrams for each component of this system. Include attachments to the ceiling. - click to see or hide solution - Solution: 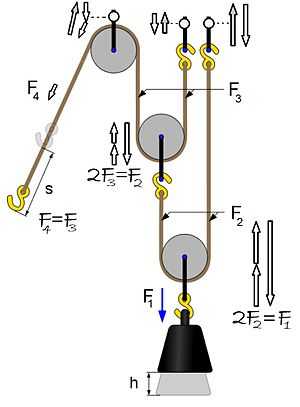 Power Pulley |
*** Problem: Motion under the influence of kinetic friction
 Let this be an object in motion, acting under friction, the normal force, and gravity. |
If this object is in motion and the coefficient of kinetic friction is μ, find the acceleration. - click to see or hide solution - Solution: This problem is unsolved. |
Links
This article is issued from Wikiversity - version of the Sunday, June 22, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.
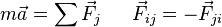
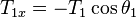 ,
,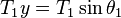
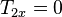 ,
,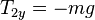
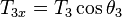 ,
,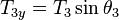
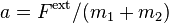 and that
and that 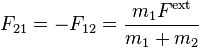 . And, the student should be able to show this without ever making the assumption that
. And, the student should be able to show this without ever making the assumption that 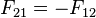 .
.