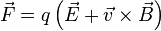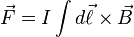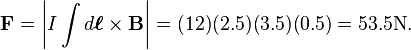Physics equations/Magnetic forces

Magnetic forces: Lorentz and Laplace]

https://en.wikipedia.org/w/index.php?title=Magnetic_field&oldid=582423833 The Lorentz force is the combination of electric and magnetic force on a point charge due to electromagnetic fields. If a particle of charge q moves with velocity v in the presence of an electric field E and a magnetic field B, then it will experience a force

\vec{F} = q\left(\vec{E} + \vec{v} \times \vec{B}\right)

(in SI units). Variations on this basic formula describe the magnetic force on a current-carrying wire (sometimes called Laplace force), the electromotive force in a wire loop moving through a magnetic field (an aspect of Faraday's law of induction), and the force on a particle which might be traveling near the speed of light (relativistic form of the Lorentz force).

If the charged particles are travelling in a wire we have the Laplace force:

\vec{F} = I\int d\vec{\ell}\times \vec{B}

Problem: A wire segment that is 2.5 meters long carries a current of 12 amps in a 3.5 Tesla field. What is the force on the segment if the angle between the wire and the magnetic field is 30 degrees? *

(click for answer)

Since sin 30° = ½, we have

\mathbf{F} = \left |I\int d\boldsymbol{\ell}\times \mathbf{B} \right |= (12)(2.5)(3.5)(0.5) = 53.5 \text{N}.

next ptoble

If 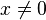$x\ne0$ , then

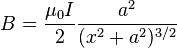B = \frac{\mu_0 I}{2} \frac{a^2}{(x^2+a^2)^{3/2}}

Here only the first (and far simpler) problem is solved. Both variants of the right-hand rule stipulate that each element of length in the line integral contributes an element of magnetic field that points in the same direction, as shown in the figures below:

References

This article is issued from Wikiversity - version of the Sunday, June 22, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.