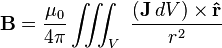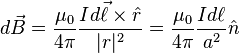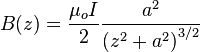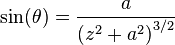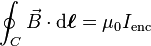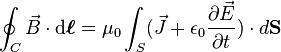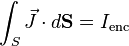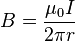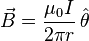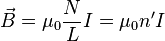Physics equations/Magnetic field calculations
< Physics equationsThe Biot-Savart law
.jpg)
The Biot–Savart law is used for computing the resultant magnetic field B at position r generated by a steady current I (for example due to a wire): a continual flow of charges which is constant in time and the charge neither accumulates nor depletes at any point. The law is a physical example of a line integral: evaluated over the path C the electric currents flow. The equation in SI units is:
**Problem: Generalize this line integral to a volume integral involving current density.
Let J be the current density vector, and let dA be a vector that denotes direction and a small (differential) area. (The direction of dA is normal to the area element). Since the vectors parallel, the inner (dot) product J·dA equals the scalar product JdA. Also parallel to both J and dA is dL, an element of length along the wire. Since the normal to the area is parallel to the length, dAdL equals dV, which is the volume element. Hence IdL equals JdV, where dL and J both have direction. Thus the line integral over current becomes a volume integral:
where dV is the differential element of volume and J is the current density vector in that volume.
Magnetic field lines for typical geometries
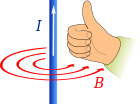 Magnetic field near a long straight wire. |
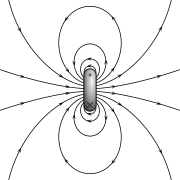 Magnetic field due to a current loop. |
 Magnetic field due to a solenoid |
Magnetic field due to a current loop
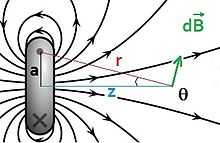
*Problem: Show that if circular loop of radius 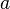 carries a current
carries a current 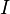 , then the the magnetic field at the center of the loop points in the
, then the the magnetic field at the center of the loop points in the 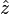 direction and as a magnitude of:
direction and as a magnitude of:
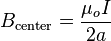 .
.
(This represents the magnetic field at  in the figure to the right; the magnetic field points in the
in the figure to the right; the magnetic field points in the 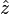 direction.)
direction.)
The distance from the source current, 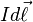 , to the field point (at the center) is always
, to the field point (at the center) is always
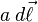 . Since
. Since 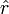 is perpendicular to
is perpendicular to 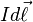 , and since their cross product always points along the axis of the loop, we have
, and since their cross product always points along the axis of the loop, we have
where 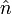 is a unit vector pointing along the axis. Since
is a unit vector pointing along the axis. Since 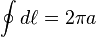 , we have our result.
, we have our result.
***Problem:Show that if circular loop of radius 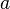 carries a current
carries a current 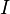 , then the the magnetic field at the at a distance
, then the the magnetic field at the at a distance 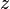 away from the center is in the z direction, has magnitude:
away from the center is in the z direction, has magnitude:
An element of the magnetic field due to an element of current is shown in the figure above and to the right. Here, 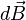 points downward because the element at the top of the loop was chosen. We seek only the
points downward because the element at the top of the loop was chosen. We seek only the 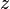 component, so we multiply by the cosine of the acute angle in the right triangle shown:
component, so we multiply by the cosine of the acute angle in the right triangle shown: 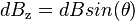 , where
, where
where z is the distance from the center of the loop. The rest of solution resembles the calculation of the magnetic field at the center of a loop.
Ampère's circuital law
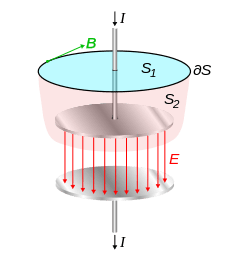
The "integral form" of the original Ampère's circuital law[1] is a line integral of the magnetic field around any closed curve C (This closed curve is arbitrary but it must be closed, meaning that it has no endpoints). The curve C bounds both a surface S, and any current which pierces that surface is said to be enclosed by the surface. The line integral of the magnetic B-field (in tesla, T) around closed curve C is proportional to the total current Ienc passing through a surface S (enclosed by C):
Maxwell's correction term (displacement current)
This equation might is not generally valid if a time-dependent electric field is present, as was discovered by James Clerk Maxwell, who added the displacement current term to Ampere's law around 1861.[2][3]
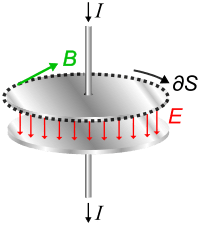
The need for this extra term can be seen in the figure to the right. The diagram shows a capacitor being charged by current 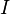 flowing through a wire, which creates a magnetic field
flowing through a wire, which creates a magnetic field 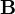 around it. The magnetic field is found from Ampere's law:
around it. The magnetic field is found from Ampere's law:
*****Problem: Show that with Maxwell's correction (with 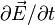 ), Ampere's law becomes:
), Ampere's law becomes:
where,
The equation says that the integral of the magnetic field 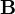 around a loop
around a loop 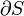 is equal to the current
is equal to the current 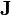 through any surface spanning the loop, plus a term depending on the rate of change of the electric field
through any surface spanning the loop, plus a term depending on the rate of change of the electric field 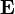 through the surface. This term, the second term on the right, is the displacement current. For applications with no time varying electric fields (unchanging charge density) it is zero and is ignored. However in applications with time varying fields, such as circuits with capacitors, it is needed, as shown below. Any surface intersecting the wire, such as
through the surface. This term, the second term on the right, is the displacement current. For applications with no time varying electric fields (unchanging charge density) it is zero and is ignored. However in applications with time varying fields, such as circuits with capacitors, it is needed, as shown below. Any surface intersecting the wire, such as 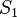 , has current
, has current 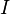 passing through it so Ampere's law gives the correct magnetic field:
passing through it so Ampere's law gives the correct magnetic field:
But surface 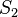 spanning the same loop that passes between the capacitor's plates has no current flowing through it, so without the displacement current term Ampere's law gives:
spanning the same loop that passes between the capacitor's plates has no current flowing through it, so without the displacement current term Ampere's law gives:
So without the displacement current term Ampere's law fails; it gives different results depending on which surface is used, which is inconsistent. The 'displacement current' term provides a second source for the magnetic field besides current; the rate of change of the electric field 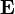 . Between the capacitor's plates, the electric field is increasing, so the rate of change of electric field through the surface
. Between the capacitor's plates, the electric field is increasing, so the rate of change of electric field through the surface 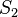 is positive, and its magnitude gives the correct value for the field field
is positive, and its magnitude gives the correct value for the field field 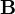 found above.
found above.
Magnetic field due to a long straight wire

*Problem: Show that in the vicinity of a long, straight wire carrying current 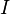 , Ampere's law yields:
, Ampere's law yields:
where 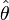 is a unit vector that points in the azimuthal direction.
is a unit vector that points in the azimuthal direction.
Do the line integral around on a circle centered around the loop. 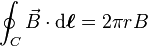
Magnetic field inside a long thin solenoid

*Problem: Show that in the vicinity of a long, thin solenoid of length 
where  is the current,
is the current, 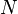 is the number of turns, and
is the number of turns, and 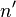 is the number of turns per unit length.
is the number of turns per unit length.
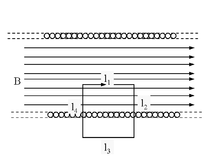
Do the line integral shown. Of the four paths,only l1 is non-zero. If /ell is the length of that path, then the total current enclosed is n'/ell
references
- ↑ https://en.wikipedia.org/w/index.php?title=Amp%C3%A8re%27s_circuital_law&oldid=578507291
- ↑ Example taken from Feynman, Richard; Robert Leighton; Matthew Sands (1964) The Feynman Lectures on Physics, Vol.2, Addison-Wesley, USA, p.18-4, using slightly different terminology.
- ↑ https://commons.wikimedia.org/w/index.php?title=File:Displacement_current_in_capacitor.svg&oldid=38260258
Basic Magnetic Terms definition with Formulas