Physics equations/Faraday law/Faraday law example

< Physics equations < Faraday law

Spinning coil in a magnetic field[1]

Faraday's law of induction|Faraday's law of electromagnetic induction states that the induced electromotive force is the negative time rate of change of magnetic flux through a conducting loop.

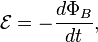
\mathcal{E} = -{{d\Phi_B} \over dt},

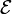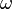where \mathcal{E} is the electromotive force (emf) in volts and ΦB is the magnetic flux in Weber (Wb)|webers. For a loop of constant area, A, spinning at an angular velocity of \omega in a uniform magnetic field, B, the magnetic flux is given by

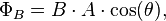
\Phi_B = B\cdot A \cdot \cos(\theta),

where θ is the angle between the normal to the current loop and the magnetic field direction. Since the loop is spinning at a constant rate, ω, the angle is increasing linearly in time, θ=ωt, and the magnetic flux can be written as

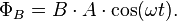
\Phi_B = B\cdot A \cdot \cos(\omega t).

Taking the negative derivative of the flux with respect to time yields the electromotive force.

\mathcal{E} = -\frac{d}{dt} \left[ B\cdot A \cdot \cos(\omega t)\right] Electromotive force in terms of derivative
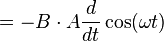= -B \cdot A \frac{d}{dt} \cos(\omega t) Bring constants (A and B) outside of derivative
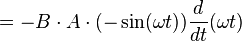=-B \cdot A \cdot (-\sin(\omega t)) \frac{d}{dt} (\omega t) Apply chain rule and differentiate outside function (cosine)
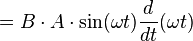= B \cdot A \cdot \sin(\omega t) \frac{d}{dt} (\omega t) Cancel out two negative signs
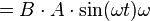= B \cdot A \cdot \sin(\omega t) \omega Evaluate remaining derivative
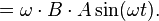= \omega \cdot B \cdot A \sin(\omega t). Simplify.

References

  1. ↑ https://en.wikibooks.org/w/index.php?title=Physics_with_Calculus/Electromagnetism/Electromagnetic_Induction&oldid=1979241
This article is issued from Wikiversity - version of the Sunday, June 22, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.