Physics equations/Collection of equations

< Physics equations

Organization: These equations are under reorganization:

Part II equations waiting to be converted into templates

Math

circumference, area, volume, elements

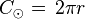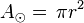
Circumference and area of circle: $C_\odot = \,2\pi r$ ; $A_\odot = \,\pi r^2$

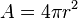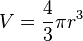
Area and volume of sphere: $A = 4\pi r^2$ ; $V = \frac{4}{3}\pi r^3$

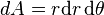
$dA = r\mathrm{d}r\,\mathrm{d}\theta$

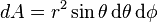
$dA = r^2 \sin\theta\, \rm d\theta\, \rm d\phi$

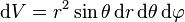
$\mathrm{d}V=r^2\sin\theta\,\mathrm{d}r\,\mathrm{d}\theta\,\mathrm{d}\varphi$

Trigonometry

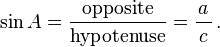
$\sin A=\frac{\textrm{opposite}}{\textrm{hypotenuse}}=\frac{a}{\,c\,}\,.$

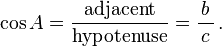
$\cos A=\frac{\textrm{adjacent}}{\textrm{hypotenuse}}=\frac{b}{\,c\,}\,.$

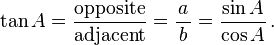
$\tan A=\frac{\textrm{opposite}}{\textrm{adjacent}}=\frac{a}{\,b\,}=\frac{\sin A}{\cos A}\,.$

Vector dot product

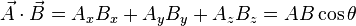
$\vec{A}\cdot \vec{B} = A_xB_x+A_yB_y+A_zB_z = AB\cos\theta$

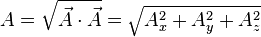
$A=\sqrt{\vec{A}\cdot \vec{A}}=\sqrt{A_x^2+A_y^2+A_z^2}$

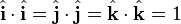
$\hat \mathbf i\cdot \hat \mathbf i = \hat \mathbf j\cdot \hat \mathbf j =\hat \mathbf k\cdot \hat \mathbf k =1$

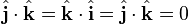
$\hat \mathbf j\cdot \hat \mathbf k = \hat \mathbf k\cdot \hat \mathbf i =\hat \mathbf j\cdot \hat \mathbf k =0$

Electromagnetism

_{from https://en.wikiversity.org/w/index.php?title=Electromagnetism_Formulae&oldid=1121007
https://en.wikiversity.org/w/index.php?title=Maxwell%27s_Equations&oldid=790747}

Before Maxwell's Equations

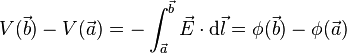
Electric field and voltage (or potential): $V(\vec b) - V(\vec a)=-\int_\vec a^\vec b \vec{E} \cdot \mathrm{d}\vec{l} = \phi(\vec b) - \phi(\vec a)$

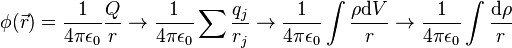
Electric potential due to point charges: $\phi(\vec r) = \frac{1}{4\pi\epsilon_0}\frac{Q}{r} \rightarrow \frac{1}{4\pi\epsilon_0} \sum \frac{q_j}{r_j}\rightarrow \frac{1}{4\pi\epsilon_0} \int \frac{\rho \mathrm{d}{V}}{r}\rightarrow\frac{1}{4\pi\epsilon_0} \int \frac{\mathrm{d}\rho}{r}$

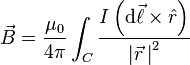
Magnetic field: $\vec{B} = \frac{\mu_0}{4\pi} \int_C \frac{I \left ( \mathrm{d} \vec{\ell} \times \hat{r} \right )}{\left | \vec{r} \,\right |^2}$

Maxwell's equations

Gauss' Law relating electric field to charge: 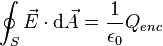$\oint_S \vec{E} \cdot \mathrm{d}\vec{A} = \frac{1}{\epsilon_0} Q_{enc}$

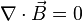
$\nabla \cdot \vec{B} = 0$

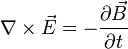
$\nabla \times \vec{E} = -\frac{\partial \vec{B}} {\partial t}$

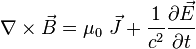
$\nabla \times \vec{B} = \mu_0\ \vec{J} + \frac{1}{c^2} \frac{\partial \vec{E}} {\partial t}$

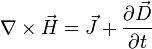
$\nabla \times \vec{H} = \vec{J} + \frac{\partial \vec{D}} {\partial t}$

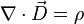
$\nabla \cdot \vec{D} = \rho$

to discard

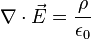
$\nabla \cdot \vec{E} = \frac{\rho}{\epsilon_0}$

Maxwell's equations integral form

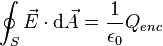
$\oint_S \vec{E} \cdot \mathrm{d}\vec{A} = \frac{1}{\epsilon_0} Q_{enc}$

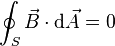
$\oint_S \vec{B} \cdot \mathrm{d}\vec{A} = 0$

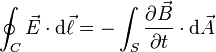
$\oint_C \vec{E} \cdot \mathrm{d}\vec{\ell} = - \int_S \frac{\partial\vec{B}}{\partial t} \cdot \mathrm{d} \vec{A}$

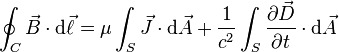
$\oint_C \vec{B} \cdot \mathrm{d}\vec{\ell} = \mu \int_S \vec{J} \cdot \mathrm{d} \vec{A} +\frac{1}{c^2} \int_S \frac{\partial\vec{D}}{\partial t} \cdot \mathrm{d} \vec{A}$

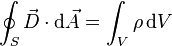
$\oint_S \vec{D} \cdot \mathrm{d}\vec{A} = \int_V \rho\, \mathrm{d}V$

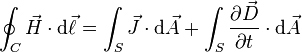
$\oint_C \vec{H} \cdot \mathrm{d}\vec{\ell} = \int_S \vec{J} \cdot \mathrm{d} \vec{A} +\int_S \frac{\partial\vec{D}}{\partial t} \cdot \mathrm{d} \vec{A}$

permittivity and magnetic permeability

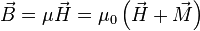
$\vec{B} = \mu\vec{H} = \mu_0 \left ( \vec{H} + \vec{M} \right )$

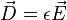
$\vec{D} = \epsilon \vec{E} = \epsilon_0 \vec{E} + \vec{P}$

$\vec{D} = \epsilon \vec{E}$

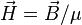
$\vec{H} = \vec{B} / \mu$

Force equations

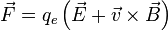
$\vec{F}=q_e\left(\vec{E}+\vec{v}\times\vec{B}\right)$

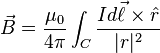
$\vec{B} = \frac{\mu_0}{4\pi}\int_C \frac{I d\vec{\ell} \times \hat r}{|r|^2}$

Current and circuits

https://en.wikibooks.org/w/index.php?title=Electronics/Formulas&oldid=2348180

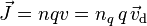
$\vec J = nqv= n_q \,q\, \vec v_\text{d}$

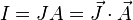
$I = JA = \vec J\cdot\vec A$

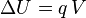
$\Delta U = q\,V$

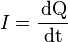
$I = \frac{\rm\,dQ}{\rm dt}$

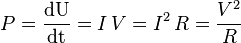
$P = \frac{\rm dU}{\rm dt}=I\,V = I^2\,R = \frac{V^2}{R}$

$V = I\,R$

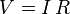
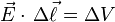
$\vec E\cdot \,\Delta\vec\ell = \Delta V$

$Q = CV$

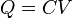
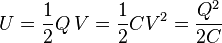
$U = \frac{1}{2}Q\,V = \frac{1}{2}CV^2 =\frac{Q^2}{2C}$

resistivity

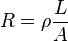
$R =\rho\frac{L}{A}$

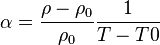
$\alpha =\frac{\rho-\rho_0}{\rho_0}\frac{1}{T-T0}$

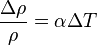$\frac{\Delta\rho}{\rho}=\alpha\Delta T$ where $\Delta\rho=\rho-\rho_0;\quad\Delta T=T-T_0\quad$

SI units

See https://en.wikipedia.org/w/index.php?title=SI_base_unit&oldid=579303285

SI units

7 Base units (https://en.wikipedia.org/w/index.php?title=International_System_of_Units&oldid=584747081)

metre m length
kilogram kg mass
second s time
ampere A electric current
kelvin K thermodynamic temperature (0°C = 273.15 K)
Mole molamount of substance (6.02214×10²³)
candela cd luminous intensity (typically 18 mW)

Derived units

radian [rad ] called: angle. units: 1 = m/m
steradian [ sr ] called: solid angle. units: 1 = m²/m²
hertz [ Hz ] called: frequency. units: s⁻¹
newton [ N ] called: force, weight. units: kg⋅m⋅s⁻²
pascal [ Pa ] called: pressure, stress. units: N/m² = kg⋅m⁻¹⋅s⁻²
joule [ J ] called: energy, work, heat. units: N⋅m = kg⋅m²⋅s⁻²
watt [ W ] called: power, radiant flux . units:J/s = kg⋅m²⋅s⁻³
coulomb [ C ] called: electric charge or quantity of electricity. units: s⋅A
volt [V ] called: voltage (electrical potential difference), electromotive force . units:W/A = kg⋅m²⋅s⁻³⋅A⁻¹
farad [ F ] called: electric capacitance . units:C/V = kg⁻¹⋅m⁻²⋅s⁴⋅A²
ohm [ Ω ] called: electric resistance, impedance, reactance. units: V/A = kg⋅m²⋅s⁻³⋅A⁻²
siemens [ S ] called: electrical conductance. units: A/V = kg−1⋅m−2⋅s3⋅A2
weber [ Wb ] called: magnetic flux. units: V⋅s = kg⋅m²⋅s⁻²⋅A⁻¹
tesla [ T ] called: magnetic field strength. units: Wb/m2 = kg⋅s−2⋅A−1
henry [ H ] called: inductance . units:Wb/A = kg⋅m²⋅s⁻²⋅A⁻²
degree [ Celsius °C] called: temperature relative to 273.15 K. units: K
lumen [ lm ] called: luminous flux . units:cd⋅sr cd
lux [ lx ] called: illuminance . units:lm/m² = m⁻²⋅cd
becquerel [ Bq] called: radioactivity (decays per unit time) . units: s⁻¹
gray [ Gy ] called: absorbed dose (of ionizing radiation). units: J/kg = m²⋅s⁻²
sievert [ Sv] called: equivalent dose (of ionizing radiation) . units:J/kg = m²⋅s⁻²
katal [ kat] called: catalytic activity . units:s⁻¹⋅mol

Advanced Physical Constants

speed of light $c \,$ =2998×10⁸m·s⁻¹

Planck constant=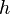 $h \,$ =6.626 × 10⁻³⁴ J·s

reduced Planck constant= 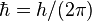$\hbar = h / (2 \pi)$ = 1.0546 × 10⁻³⁴ J·s

more constants that need sorting:

Atomic mass constant =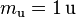 $m_{\mathrm{u}} = 1\,\mathrm{u} \,$ =1.660 538 921(73) × 10⁻²⁷ kg

Avogadro's number =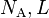 $N_{\mathrm{A}}, L \,$ =6.022 141 29(27) × 10²³ mol⁻¹ (number of atoms in a mole)

Boltzmann constant =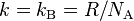 $k = k_{\mathrm{B}} = R / N_{\mathrm{A}} \,$ =1.381 × 10⁻²³ J·K⁻¹ (converts Kelvins to Joules)

gas constant =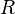 $R \,$ =8.31446 J·K⁻¹·mol⁻¹ (converts Kelvins to Joules per mole)

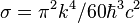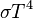
Stefan–Boltzmann constant = $\sigma = \pi^2 k^4 / 60 \hbar^3 c^2$ =5.670 373(21) × 10⁻⁸ W·m⁻²·K⁻⁴ (black body power per unit area is $\sigma T^4$

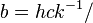Wien displacement law constant (needs to be better defined in terms of maximum lambda and temperature) $b = h c k^{-1} / \,$ 4.965 114 231... =2.897 7721(26) × 10⁻³ m·K

References

This article is issued from Wikiversity - version of the Saturday, January 30, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.