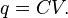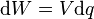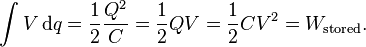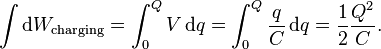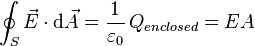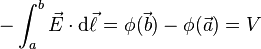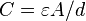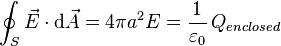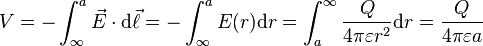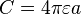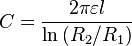Physics equations/Capacitors

Capacitance

from https://en.wikipedia.org/w/index.php?title=Capacitance&oldid=581221622

Capacitance is the ability of a body to store an electrical charge. Any object that can be electrically charged exhibits capacitance. We shall consider capacitors that are linear, meaning that there is direct proportionality between charge, q, and voltage, V {where is the electric potential):

q =CV.

The SI unit of capacitance is the farad (symbol: F), named after the English physicist Michael Faraday. The most common subunits of capacitance in use today are the microfarad (µF), nanofarad (nF), picofarad (pF), and, in microcircuits, femtofarad (fF). However, specially made supercapacitors can be much larger (as much as hundreds of farads), and parasitic capacitive elements can be less than a femtofarad.

The energy (measured in joules) stored in a capacitor is equal to the work done to charge it. Consider a capacitor of capacitance C, holding a charge +q on one plate and −q on the other. Moving a small element of charge dq from one plate to the other against the potential difference V = q/C requires the work dW:

\mathrm{d}W = V \mathrm{d}q

where W is the work measured in joules, q is the charge measured in coulombs and C is the capacitance, measured in farads. This can be integrated to yield a final stored energy equal to:

\int V \,\mathrm{d}q = \frac{1}{2}\frac{Q^2}{C} = \frac{1}{2}QV = \frac{1}{2}CV^2 = W_\text{stored}.

The energy stored in a capacitor is found by integrating this equation.

Problem: Perform this integration.

Solution

Starting with an uncharged capacitance (q = 0) and moving charge from one plate to the other until the plates have charge +Q and −Q requires the work W:

\int\mathrm{d}W_\text{charging} = \int_0^Q V \, \mathrm{d}q = \int_0^Q \frac{q}{C} \, \mathrm{d}q = \frac{1}{2}\frac{Q^2}{C}.

Using Q =CV (for the fully charged capacitor) we obtain the the other forms by substitution: ½Q²/C = ½QV =½CV².

Capacitances of simple systems

Table of Capacitances

Capacitance of simple systems
Type	Capacitance	Comment
Parallel-plate capacitor	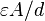$\varepsilon A /d$	ε: Permittivity
Coaxial cable	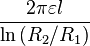$\frac{2\pi \varepsilon l}{\ln \left( R_{2}/R_{1}\right) }$	ε: Permittivity
Pair of parallel wires	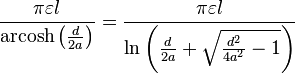$\frac{\pi \varepsilon l}{\operatorname{arcosh}\left( \frac{d}{2a}\right) }=\frac{\pi \varepsilon l}{\ln \left( \frac{d}{2a}+\sqrt{\frac{d^{2}}{4a^{2}}-1}\right) }$
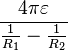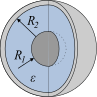
Concentric spheres	$\frac{4\pi \varepsilon}{\frac{1}{R_1}-\frac{1}{R_2}}$	ε: Permittivity
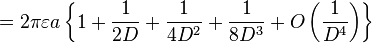Two spheres, equal radius	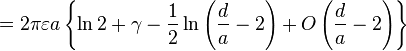$=2\pi \varepsilon a\left\{ 1+\frac{1}{2D}+\frac{1}{4D^2}+\frac{1}{8D^{3}}+O\left( \frac{1}{D^{4}}\right) \right\}$ $=2\pi \varepsilon a\left\{ \ln 2+\gamma -\frac{1}{2}\ln \left( \frac{d}{a}-2\right) +O\left( \frac{d}{a}-2\right) \right\}$	a: Radius d: Distance, d > 2a D = d/2a γ: Euler's constant
Sphere	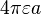$4\pi \varepsilon a$	a: Radius
Circular disc	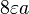$8\varepsilon a$	a: Radius
Thin straight wire, finite length	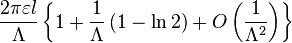$\frac{2\pi \varepsilon l}{\Lambda }\left\{ 1+\frac{1}{\Lambda }\left( 1-\ln 2\right) +O\left(\frac{1}{\Lambda ^{2}}\right) \right\}$	a: Wire radius l: Length Λ: ln(l/a)

Problems

Problem: Show that the Capacitance of a parallel plate capacitor is 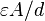$\varepsilon A /d$ , where A is plate area and d is the distance between the plates.

Solution

This solution requires that you already "know" a few facts about the system, which we shall state without proof.

There is no net charge on the plates (with positive Q on one plate and negative Q on the other).
The charge is uniformly distributed over each plate.
The electric field exists only between the plates.

Use Gauss' Law to find the electric field

\oint_S\vec{E} \cdot\mathrm{d}\vec{A} = \frac{1}{\varepsilon_0}\,Q_{enclosed}= EA

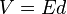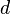This equation establishes that $V = Ed$ , where $E$ and $d$ is the gap between the plates:

-\int_a^b{\vec{E}\cdot \mathrm{d}\vec \ell} = \phi (\vec b) -\phi(\vec a) = V

(It is customary to denote the electric potential, 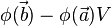$\phi (\vec b) -\phi(\vec a) V$ , as the "voltage", 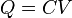$Q=CV$ . "voltage". Use the definition of capactance, 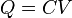$Q=CV$ , to obtain,

C =\varepsilon A /d

Problem: Show that the capacitance of an isolated sphere is 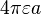$4\pi \varepsilon a$ , where a is radius.

Solution

By Gauss' Law, the electric field is found by solving

\oint_S\vec{E} \cdot\mathrm{d}\vec{A} = 4\pi a^2 E= \frac{1}{\varepsilon_0}\,Q_{enclosed}

After solving this for E, we integrate to find the potential on the surface of a sphere of radius a.

V = -\int_\infty^a{\vec{E}\cdot \mathrm{d}\vec \ell} = -\int_\infty^a {E(r)\mathrm{d}r} = \int_a^\infty{\frac{Q}{4\pi\varepsilon r^2}\mathrm{d}r} = \frac{Q}{4\pi\varepsilon a}

Use the definition of capacitance, 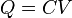$Q=CV$ , to obtain,

C = 4\pi \varepsilon a

Problem: Show that if the outer and inner radii of two concentric sphere is, 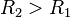$R_2 > R_1$ , the capacitance is

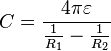C = \frac{4\pi \varepsilon}{\frac{1}{R_1}-\frac{1}{R_2}}

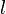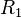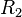Problem: Show that if the length of a long coaxial cable is, , $l$ , and the inner and outer radii are $R_{1}$ and $R_{2}$ , respectively, then the capacitance is,

C = \frac{2\pi \varepsilon l}{\ln \left( R_{2}/R_{1}\right) }

References

This article is issued from Wikiversity - version of the Sunday, February 23, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.