Physics equations/18-Electric charge and field/A:ElectricFieldGravityCompare

This is a good warmup activity before a lab:

Consider the electric and gravitational fields for the electron in the hydrogen atom at Earth's surface

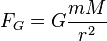F_G =G\frac{mM}{r^2}\, , where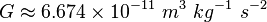 G \approx 6.674 \times 10^{-11} \ m^3 \ kg^{-1} \ s^{-2}
Calculate the ratio of gravity to electrical forces for a proton and an electron separated by distance equal to the Bohr radius, 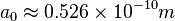a_0 \approx 0.526\times 10^{-10}m , with the electron mass 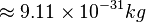\approx 9.11\times 10^{-31}kg, and the proton mass 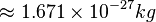\approx 1.671\times 10^{-27}kg. The ratio F/FG is about 2x1039, a large large number.
  1. Perform this calculation.
  2. What does this say about the importance of Earth's gravity in calculating electron energy levels?
This article is issued from Wikiversity - version of the Tuesday, June 03, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.