Physics equations/08-Linear Momentum and Collisions
< Physics equationsCALCULUS-based generalization to non-uniform force
Here we use the Riemann sum to clarify what happens when the force is not constant.
If the force is not constant, we can still use 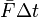 as the impulse, with the understanding that
as the impulse, with the understanding that 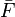 represents a time average. Recall that the average of a large set of numbers is the sum divided by the
represents a time average. Recall that the average of a large set of numbers is the sum divided by the 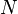 :
:
With a bit of algebra, we can turn this into a Riemann sum.
For a collision that occurs over a finite time interval, 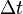 , we break that collision time into much smaller intervals
, we break that collision time into much smaller intervals 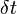 . The former might be the collision time between a golf ball and the club, while the latter would be the time interval of an ultra high-speed camera. Note that
. The former might be the collision time between a golf ball and the club, while the latter would be the time interval of an ultra high-speed camera. Note that 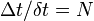 , where
, where 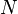 is the number of frames of the camera. Let
is the number of frames of the camera. Let 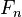 be the force associated with the n-th frame. The discretely defined average force associated with that camera is:
be the force associated with the n-th frame. The discretely defined average force associated with that camera is:
Footnote: This conversion from discrete to continuous math is easy to grasp, although the details are difficult to master: Other examples of this method include:
- Descrete and continuous expection values.
- The Discrete Fourier transform, the Fourier series, and the Fourier transform
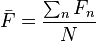
![\bar F \Delta t=\frac {\sum_n F_n}{N} \cdot \Delta t
= \sum_{n=1}^N \left[ F_n \cdot
\left\{ \frac{\Delta t / \delta t}{N} \right\}
\cdot \delta t \right]
= \sum_{n=1}^N F_n
\cdot \delta t
\rightarrow \int_0^{\Delta t}F(t)\,dt](../I/m/f59f8829dccac707da0f063fae4a8f46.png)