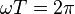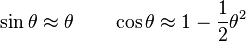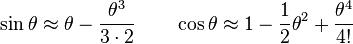Physics equations/07-Work and Energy/A:pendulum

Wikilab: Energy and the pendulum

By definition, angular frequency and period are related by,

\omega T = 2\pi

This lab employs two approximation that are valid when 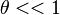$\theta<<1$ :

\sin\theta\approx\theta \qquad \cos\theta\approx 1-\frac{1}{2} \theta ^2

Use the Excel spreadsheet to plot the sine and cosine functions for θ between zero and one, taking approximately 20 increments within that interval.

Copy and paste your page onto the same excel spreadsheet and verify that a better approximation is:

\sin\theta\approx\theta -\frac{\theta^3}{3\cdot2}\qquad \cos\theta \approx 1-\frac{1}{2}\theta^2 + \frac{\theta^4}{4!}

Consider a pendulum of length L situated so that the equilibrium point is at the origin. Make a careful hand drawing showing that:

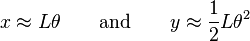
$x\approx L\theta\qquad\mathrm{and} \qquad y\approx \frac 1 2 L\theta^2$

Use this to show that an approximate formula for the energy of a pendulum is:

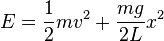
$E = \frac 1 2 mv^2 + \frac{mg}{2L}x^2$

Defining 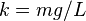$k= mg/L$ as the effective spring constant, this energy can be expressed in familiar form:

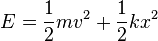
$E = \frac 1 2 mv^2 + \frac{1}{2}kx^2$

This article is issued from Wikiversity - version of the Wednesday, May 07, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.