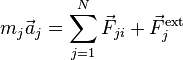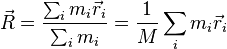Physics equations/04-Dynamics: Force and Newton's Laws/A:practice
Newton's third law
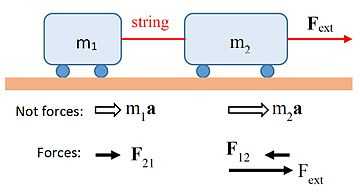 Two carts are connected by a string; a force is applied to one. By Newton's third law, the force on 1 by 2 equals the force on 2 by t. But we do not need Newton's third law to solve this problem. |
Consider two carts of mass known masses (m1 and m2) connected by a taught string, with one mass (m2) experiencing and external force of known magnitude. Assume that the collection of objects held together by a taught string obeys F=(m1+m2)a where F is the sum of all external forces. But we do not assume that string (in the middle) exerts equal and opposite forces on the two objects. (In this way we prove Newton's third law.) - click to see or hide solution - Solution: We take the acceleration, as well as the two internal forces as unknowns (we have three unknowns because we make no assumption about the equality of the two internal forces transmitted by the string, which we assume to have negligible mass. With three unknowns, we seek three equations. Beginning with Newton's second law (ΣF=ma) applied to and M=m1+m2, we have:
(They all have the same acceleration because the string is assumed taught.)
|
Pulleys
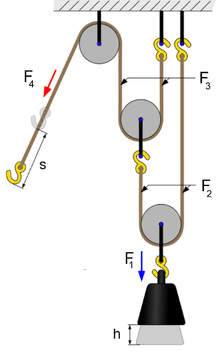 Power Pulley |
Make free body diagrams for each component of this system. Include attachments to the ceiling. - click to see or hide solution - Solution: 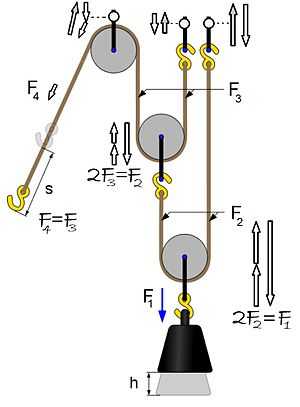 Power Pulley |
Newton's third law
Simple statement of Newton's third law
This popular statement of Newton's third law is somewhat misleading because the word "force" should be substituted for "action":
For every "action" there is and equal and opposite "reaction".
Also, this statement fails to emphasize that the two forces ALWAYS act on different objects. When making a free-body diagram with two or more objects, each object gets its own free body diagram.
Advanced statement of Newton's third law
The forces on a collection of N interacting particles can be described as either internal or external forces. Since forces are generally viewed as interactions between particles, the external force on the j-th particle, 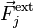 is an interaction with particles outside this collection of N particles. The sum of all forces on the jth particle is:
is an interaction with particles outside this collection of N particles. The sum of all forces on the jth particle is:
Newton's third law states that the internal force on the jth particle by the ith particle is 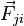 , and Newton's third law states that
, and Newton's third law states that 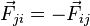 . Since the only number that equals its additive inverse is zero, it follows that no particle can exert a force on itself, e.g.
. Since the only number that equals its additive inverse is zero, it follows that no particle can exert a force on itself, e.g. 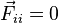 (for all i), and one wonders if the motion of physical objects could ever have been fathomed if particles could induce forces on themselves. When many particles are connected (either rigidly or by forces that allow relative motion), it can be shown that Newton's second law (F-ma) applies to the center-of-mass, defined as:
(for all i), and one wonders if the motion of physical objects could ever have been fathomed if particles could induce forces on themselves. When many particles are connected (either rigidly or by forces that allow relative motion), it can be shown that Newton's second law (F-ma) applies to the center-of-mass, defined as:
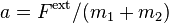 and that
and that 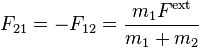 . And, the student should be able to show this without ever making the assumption that
. And, the student should be able to show this without ever making the assumption that 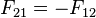 .
.