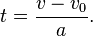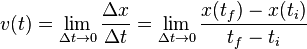Physics equations/02-One dimensional kinematics/A:practice
The solutions are available. Click to show.
Highway exits
A driver gets on mile 25 of a highway at 3:30 pm and exits at mile 150 at 5:30 pm. If the road is straight, what is the velocity and is it average or instantaneous?
Solution: 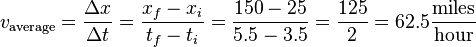
It is an average velocity because the time interval is not infinitesimally small. (In physics we like to be precise and call it velocity and not speed because if the person was going in the opposite direction, the result would have been negative. Velocity has direction as a property, speed does not.
Finding average velocity
A particle starting 23 m from the origin has moved to 43 m in 5 s. Find 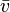 .
.
Solution: 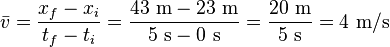
Finding the average acceleration if the direction reverses in the time interval
A person is jogging east at 3m/s when he suddenly reverses direction and is jogging west at 3m/s, taking one second to accomplish this reversal. Take east to be the 'positive' direction. What is the average acceleration?
Solution: 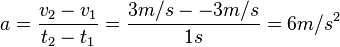
Wait a minute! East is postive and west is negative. There is a minus sign error
Proving one of the equations of motion
Use algebra to show that
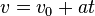 and
and 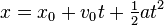
implies
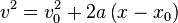 and
and 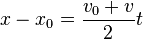 .
.
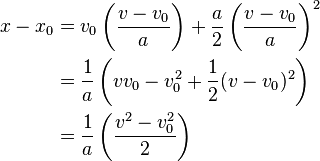
Solution: Solve 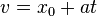 to obtain,
to obtain,
Insert this into
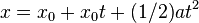 to obtain,
to obtain,Therefore,
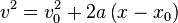 . Also,
. Also, 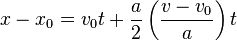 yields
yields 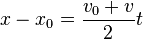 .
. Does this mean that the average velocity,
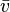 equals
equals 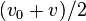 ? Yes, but only if the acceleration is uniform.
? Yes, but only if the acceleration is uniform. -
CALCULUS: Motion and the mathematical definition of derivative as a limit
By definition, velocity involves two different positions at two different times. However, we may take the limit that these differences are very small and define the instantaneous velocity.
A connection to differential calculus is seen by rewriting 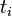 and
and 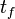 as
as 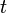 and
and 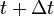 , so that
, so that 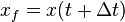 :
:
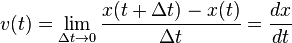
CALCULUS: Problem involving velocity, acceleration, and equations of motion
A particle's motion[1]
is described by the equation 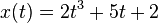 . Find
. Find
a) the particle's velocity function,
b) its instantaneous velocity at t = 2 s. Also find
c) the particle's acceleration function and
d) its instantaneous acceleration at t = 2 s.
Solution First we note that the coefficients need units (these units are often omitted when calculating informally): ![x(t) = 2\left [\frac{\mathrm{m}}{\mathrm{s}^3}\right ]\ t^3 +
5\left [\frac{\mathrm{m}}{\mathrm{s}^2}\right ]\ t +
2\ \mathrm{m}\](../I/m/4a61c5ce3a47636ce9c020fb65d17662.png)
a)
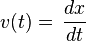
![=
\,\frac{d}{dt} \left (
2\left [\frac{\mathrm{m}}{\mathrm{s}^3}\right ]\ t^3 +
5\left [\frac{\mathrm{m}}{\mathrm{s}}\right ]\ t +
2\ \mathrm{m}\ \right )](../I/m/2ac3f25b3366e6a2553d5a27b114d42d.png)
![=
\underline{\overline{ \left |
6 \left [\frac{\mathrm{m}}{\mathrm{s}^3}\right ]\ t^2 +
5\left [\frac{\mathrm{m}}{\mathrm{s}}\right ]
\right |}}](../I/m/4182c649d73a6689cfb0f838452a2be6.png)
b)
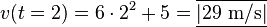
c)
![a(t) = \,\frac{d}{dt} \left (6 \left [\frac{\mathrm{m}}{\mathrm{s}^3}\right ]\ t^2 +
5\left [\frac{\mathrm{m}}{\mathrm{s}}\right ] \right ) =
\underline{\overline{ \left |
12\left [\frac{\mathrm{m}}{\mathrm{s^3}}\right ]t
\right |}}](../I/m/67f1fa0af82af3e79795ae30685f5744.png)
d)
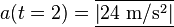
- ↑ https://en.wikibooks.org/w/index.php?title=Physics_with_Calculus/Mechanics/Motion_in_One_Dimension&oldid=2403866