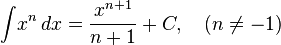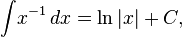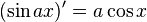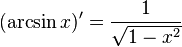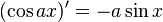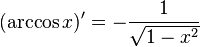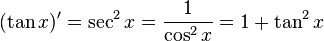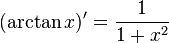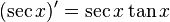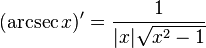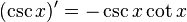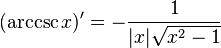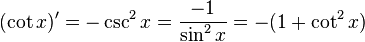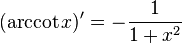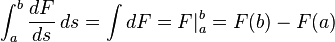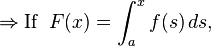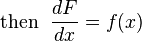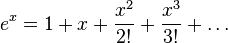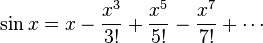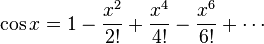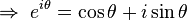Physics equations/01-Introduction/A:reviewCALCULUS

Calculus[1]

If f and g are functions of x and a and b are constants, then: 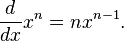  \frac{d}{dx} x^n = nx^{n-1}.           

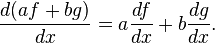
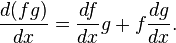
\frac{d(af+bg)}{dx} = a\frac{df}{dx} +b\frac{dg}{dx}.           \frac{d(fg)}{dx} = \frac{df}{dx} g + f \frac{dg}{dx}.           


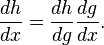
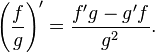
\frac{dh}{dx} = \frac{dh}{dg} \frac{dg}{dx}.           \left(\frac{f}{g}\right)' = \frac{f'g - g'f}{g^2}.

If y=y(x) and x=x(y) are inverse functions then: 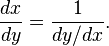\frac{dx}{dy} = \frac{1}{dy/dx}.

Indefinite integrals, where 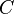C is the arbitrary constant of integration:

\int\! x^n \,dx= \frac{ x^{n+1}}{n+1} + C, \quad (n \neq -1)
\int \! x^{-1}\, dx= \ln |x|+C,

Exponential and trigonometric functions

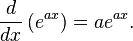
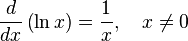
If a is a constant, then: 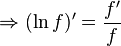\frac{d}{dx}\left(e^{ax}\right) = ae^{ax}.              \frac{d}{dx}\left( \ln x\right) = {1 \over x} ,\quad x \ne 0    \Rightarrow(\ln f)'= \frac{f'}{f} \quad wherever f is positive.

(\sin ax)' = a\cos x \, (\arcsin x)' = { 1 \over \sqrt{1 - x^2}} \,
(\cos ax)' = -a\sin x \, (\arccos x)' = -{1 \over \sqrt{1 - x^2}} \,
(\tan x)' = \sec^2 x = { 1 \over \cos^2 x} = 1 + \tan^2 x \, (\arctan x)' = { 1 \over 1 + x^2} \,
(\sec x)' = \sec x \tan x \, (\operatorname{arcsec} x)' = { 1 \over |x|\sqrt{x^2 - 1}} \,
(\csc x)' = -\csc x \cot x \, (\operatorname{arccsc} x)' = -{1 \over |x|\sqrt{x^2 - 1}} \,
(\cot x)' = -\csc^2 x = { -1 \over \sin^2 x} = -(1 + \cot^2 x)\, (\operatorname{arccot} x)' = -{1 \over 1 + x^2} \,

Fundamental theorem of calculus

\int_{a}^b \frac {dF}{ds}\,ds= \int dF = F|_a^b=F(b)-F(a)
\Rightarrow \text{If }\;F(x)=\int_{a}^x f(s)\,ds,\,   \text{ then }\;\frac {dF}{dx}=f(x)

Taylor series and Euler's equations[2]

e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \dots
\sin x = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots
\cos x = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \cdots
\Rightarrow \; e^{i \theta} = \cos \theta + i\sin\theta
This article is issued from Wikiversity - version of the Wednesday, February 24, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.