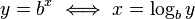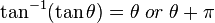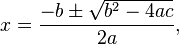Physics equations/01-Introduction/A:mathReview

Common misconceptions

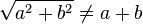$\left(\frac 1 x + \frac 1 y\right)^{-1}\ne x+y$ and $\sqrt{a^2+b^2}\ne a+b$ .

Percent

The 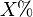$X%$ symbol means 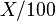$X/100$ . A quick and dirty way to find the percent difference is to divide the big number by the small:

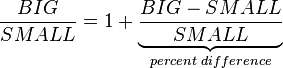
$\frac{BIG}{SMALL}=1+\underbrace{\frac{BIG-SMALL}{SMALL}}_{percent\; difference}$

Trigonometry

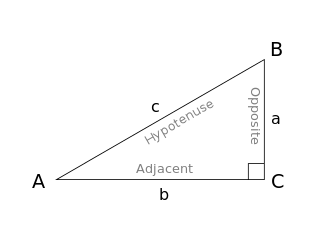
In this right triangle: sin A = a/c; cos A = b/c; tan A = a/b.

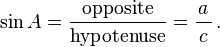
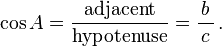
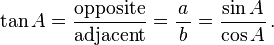
$\sin A=\frac{\textrm{opposite}}{\textrm{hypotenuse}}=\frac{a}{\,c\,}\,.$ $\cos A=\frac{\textrm{adjacent}}{\textrm{hypotenuse}}=\frac{b}{\,c\,}\,.$ $\tan A=\frac{\textrm{opposite}}{\textrm{adjacent}}=\frac{a}{\,b\,}=\frac{\sin A}{\cos A}\,.$

Logarithms and exponents are inverse functions

y = b^x \iff x = \log_b y

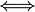The $\iff$ implies that the statements are equivalent.

The three most common bases are 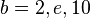$b = 2, e, 10$ .

The natural log is defined as 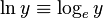$\ln y \equiv \log_e y$ .

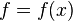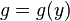If $f=f(x)$ and $g=g(y)$ are inverse functions, then:

g(f(x))=x

and

f(g(y))=y

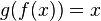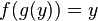, and we write:

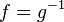$f = g^{-1}$ and $g = f^{-1}$ .

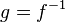Warning: Do not be confused about this notations. The inverses are NOT multiplicative inverses:

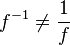f^{-1} \ne \frac 1 f

Complexities occur when the inverse is not a true function, or equivalently, when the inverse is multi-valued:

\tan^{-1}(\tan \theta) = \theta\; or\; \theta+\pi

Here the problem arises because,

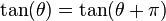\tan(\theta)=\tan(\theta+\pi)

so that knowing the tangent of angle does not precisely tell you what the angle was.

\tan^{-1}

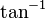is called the 'arctangent', or the 'inverse tangent'.

\sin^{-1}

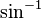is called 'arcsine', or the 'inverse sine' and so forth.

Quadratic equation

This quadratic equation, 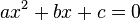$ax^2 + bx + c = 0$ , has the solutions:

x=\frac{-b \pm \sqrt {b^2-4ac}}{2a},

Factoring

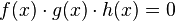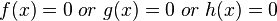
If $f(x)\cdot g(x)\cdot h(x) = 0$ then $f(x) =0\;or\;g(x)=0\;or\;h(x)=0$

Example:

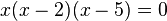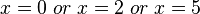
If $x(x-2)(x-5)=0$ then $x=0\;or\;x=2\;or\;x=5$

This article is issued from Wikiversity - version of the Wednesday, May 07, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.