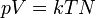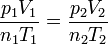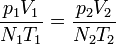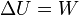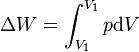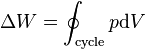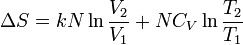Physics Formulae/Thermodynamics Formulae
< Physics FormulaeLead Article: Tables of Physics Formulae
This article is a summary of the laws, principles, defining quantities, and useful formulae in the analysis of Thermodynamics.
Thermodynamics Laws
| Zeroth Law of Thermodynamics | 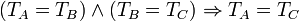
(systems in thermal equilibrium) |
| First Law of Thermodynamics | 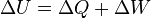
Internal energy increase Heat energy transferred to system Work done transferred to system |
| Second Law of Thermodynamics | 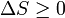 |
| Third Law of Thermodynamics | 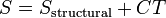 |
Thermodynamic Quantities
| Quantity (Common Name/s) | (Common Symbol/s) | Defining Equation | SI Units | Dimension |
|---|---|---|---|---|
| Number of Molecules | 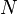 |
dimensionless | dimensionless | |
| Temperature | 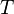 |
K | [Θ] | |
| Heat Energy | 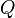 |
J | [M][L]2[T]-2 | |
| Latent Heat | 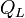 |
J | [M][L]2[T]-2 | |
| Entropy | 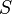 |
J K-1 | [M][L]2[T]-2 [Θ]-1 | |
| Heat Capacity (isobaric) | 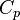 |
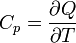 |
J K -1 | [M][L]2[T]-2 [Θ]-1 |
| Specific Heat Capacity (isobaric) | 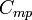 |
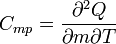 |
J kg-1 K-1 | [L]2[T]-2 [Θ]-1 |
| Molar Specific Heat
Capacity (isobaric) |
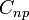 |
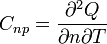 |
J K -1 mol-1 | [M][L]2[T]-2 [Θ]-1 [N]-1 |
| Heat Capacity (isochoric) | 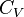 |
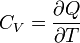 |
J K -1 | [M][L]2[T]-2 [Θ]-1 |
| Specific Heat Capacity (isochoric) | 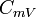 |
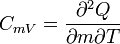 |
J kg-1 K-1 | [L]2[T]-2 [Θ]-1 |
| Molar Specific Heat
Capacity (isochoric) |
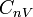 |
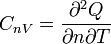 |
J K -1 mol-1 | [M][L]2[T]-2 [Θ]-1 [N]-1 |
| Internal Energy
Sum of all total energies which constitute the system |
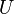 |
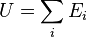 |
J | [M][L]2[T]-2 |
| Enthalpy | 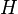 |
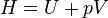 |
J | [M][L]2[T]-2 |
| Gibbs Free Energy | 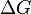 |
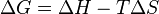 |
J | [M][L]2[T]-2 |
| Helmholtz Free Energy | 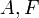 |
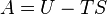 |
J | [M][L]2[T]-2 |
| Specific Latent Heat | 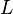 |
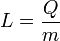 |
J kg-1 | [L]2[T]-2 |
| Ratio of Isobaric to
Isochoric Heat Capacity, Adiabatic Index |
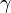 |
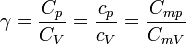 |
dimensionless | dimensionless |
| Linear Coefficient of Thermal Expansion | 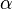 |
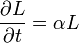 |
K-1 | [Θ]-1 |
| Volume Coefficient of Thermal Expansion | 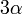 |
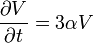 |
K-1 | [Θ]-1 |
| Temperature Gradient | No standard symbol | 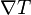 |
K m-1 | [Θ][L]-1 |
| Thermal Conduction Rate/
Thermal Current |
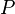 |
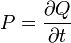 |
W = J s-1 | [M] [L]2 [T]-2 |
| Thermal Intensity | 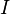 |
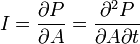 |
W m-2 | [M] [L]-1 [T]-2 |
| Thermal Conductivity | 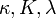 |
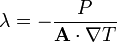 |
W m-1 K-1 | [M] [L] [T]-2 [Θ]-1 |
| Thermal Resistance | 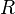 |
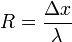 |
m2 K W-1 | [L] [T]2 [Θ]1 [M]-1 |
| Emmisivity Coefficient |  |
Can only be found from experiment
(true black body) |
dimensionless | dimensionless |
Kinetic Theory
| Ideal Gas Law | 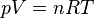
|
| Translational Energy | 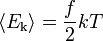 |
| Internal Energy | 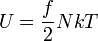 |
Thermal Transitions
| Adiabatic | 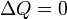
|
| Work by an Expanding Gas | Process
|
| Isobaric Transition | 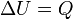 |
| Cyclic Process | 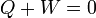 |
| Work, Isochoric | 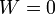 |
| work, Isobaric | 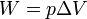 |
| Work, Isothermal | 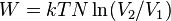 |
| Adiabatic Expansion | 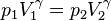
|
| Free Expansion | 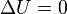 |
Statistical Physics
Below are usefull results from the Maxell-Boltzmann distribution for an ideal gas, and the implications of the Entropy quantity.
| Degrees of Freedom | 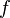 |
| Maxwell-Boltzmann Distribution,
Mean Speed |
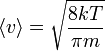 |
| Maxwell-Boltzmann Distribution
Mode-Speed |
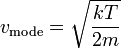 |
| Root Mean Square Speed | 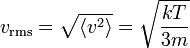 |
| Mean Free Path | 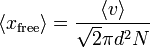 ? ? |
| Maxwell–Boltzmann Distribution | 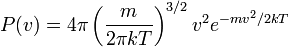 |
| Multiplicity of Configurations | 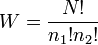 |
| Microstate in one half of the box | 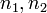 |
| Boltzmann's Entropy Equation | 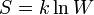 |
| Irreversibility |  |
| Entropy | 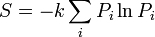 |
| Entropy Change | 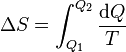
|
| Entropic Force | 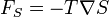 |
Thermal Transfer
| Stefan-Boltzmann Law | 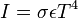 |
| Net Intensity Emmision/Absorbtion |  |
| Internal Energy of a Substance | 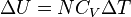 |
| Work done by an Expanding Ideal Gas | 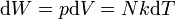 |
| Meyer's Equation | 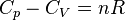 |
Thermal Efficiencies
| Engine Efficiency | 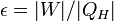 |
| Carnot Engine Efficiency | 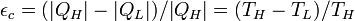 |
| Refrigeration Performance | 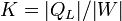 |
| Carnot Refrigeration Performance | 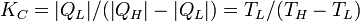 |
This article is issued from Wikiversity - version of the Friday, July 17, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.
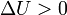 , decrease
, decrease 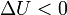
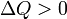 , from system
, from system 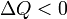
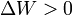 by system
by system 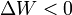
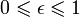
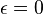 for perfect reflector
for perfect reflector for perfect absorber
for perfect absorber