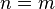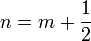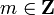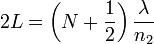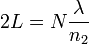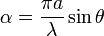Physics Formulae/Equations of Light
< Physics FormulaeLead Article: Tables of Physics Formulae
This article is a summary of the laws, principles, defining quantities, and useful formulae in the analysis of photonics.
Geometric Optics
Definitions, Quantities
Definitions
For conveinece in the table below, "r-surface" refers to reflecting/refracting surface. This is not a standard abbreviation.
| Quantity (Common Name/s) | (Common) Symbol/s | Defining Equation | SI Units | Dimension |
|---|---|---|---|---|
| Refractive Index of substance | n | 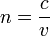
|
dimensionless | dimensionless |
| Object Distance | s | m | [L] | |
| Image Distance | s' | m | [L] | |
| Focal Length | f | m | [L] | |
| Optcal Power | P | 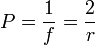 |
D (Dipotres) = m-1 | [L]-1 |
| Radius of Curvature
of r-surface |
f | m | [L] | |
| Lateral Magnification | m | 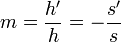
m and h negative when upside down |
dimensionless | dimensionless |
| Angular Magnification | m | 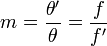 |
dimensionless | dimensionless |
| Dispersive Power | ω | 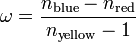
by the frequencies of the Fraunhöfer lines. |
dimensionless | dimensionless |
Sign Conventions and Implications
There are different sign conventions which can be used, perhaps the the simplist to understand and recall is the one below[1].
The general pattern is the following:
Distances for real rays of light actually traversed are positve
Distances for apparent (i.e. virtual) rays of light not actually traversed are negative.
Distances are measured to the the apex of the r-surface on the optic axis.
| Quantity | + | - |
|---|---|---|
| s | Object in front of r-surface | Object behind r-surface |
| s' | Real image | Virtual image |
| f, P | Converging r-surface | Diverging r-surface |
| r | r-surface centre of curvature
on same side as object |
r-surface centre of curvature
on opposite side as object |
Laws of Geomtric Optics
| Law of Reflection | 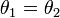 |
| Snell's Law of Refraction,
Angles of Refraction |
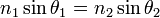 |
Mirrors
| Image distance in a Plane Mirror | 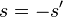 |
| Image distance in a Spherical Mirror | 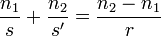 |
| Spherical Mirror Focal Length | 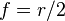 |
| Spherical Mirror | 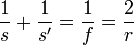 |
General Media
| Critical Angle of Total Internal Reflection | 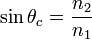 |
Lenses
| Thin Lens, Focal Length | 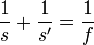
|
| Newton's Formula | 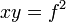
|
Prisms
| Minimum Deviation Angle
D = Deviation Angle |
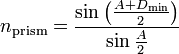
|
Radiometry
| Quantity (Common Name/s) | (Common) Symbol/s | Defining Equation | SI Unit | Dimension |
|---|---|---|---|---|
| Radiant Power | Q | J = | [M] [L]2 [T]-2 | |
| Radiant Flux, Radiant Power | Φ | W | ||
| Radiant Intensity | I | W sr-1 | [M] [L]2 [T]-3 | |
| Radiance, Radiant Intensity | L | W sr-1 m-2 | ||
| Irradiance, Incident Intensity,
Intensity incident on a surface |
E, I | W sr-1 m-2 | ||
| Radiant Exitance, Radiant Emittance | M | W m-2 | ||
| Radiosity (heat transfer), Radiosity, emitted plus
reflected Intensity leaving a surface |
J, Jλ | W m-2 | ||
| Spectral Radiance | Lλ, Lν | W sr-1 m-3 = W sr-1 Hz-2 | ||
| Spectral Irradiance | Eλ, Eν | W m-3 = W m-2 Hz-1 | ||
Photometry
| Quantity (Common Name/s) | (Common) Symbol/s | Defining Equation | SI Units | Dimension |
|---|---|---|---|---|
| Luminous energy | Qv | J = lm s | [M] [L]2 [T]-2 | |
| Luminous flux, luminous power | F, Φv | cd sr = lm = J s-1 | [Φ] | |
| Luminous intensity | Iv | cd = lm sr-1 | [Φ] | |
| Luminance | Lv | cd m-2 | [Φ] [L]-2 | |
| Illuminance (light incident on a surface) | Ev | lx = lm m-2 | [Φ] [L]-2 | |
| Luminous Emittance (light emitted from a surface | Mv | lx = lm m2 | [Φ] [L]-2 | |
| Luminous efficacy | 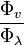 |
lm W-1 | [Φ] [T]2 [M]-1 [L]-2 | |
Physical Optics
Luminal EM Waves
| Electric Field Component | 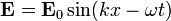 | |
| Magnetic Field Component | 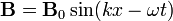 | |
| Luminal Speed in Meduim | 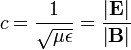 | |
| Poynting Vector | 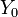 = Admittance of Free Space = Admittance of Free Space
|
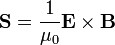
|
| Poynting Vector Magnitude | 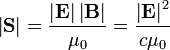 | |
| Root Mean Square Electric Field of Light | 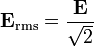 | |
| Irradiance, Light Intensity | 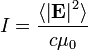 | |
| Irradiance, Light Intensity
due to a Point Source |
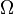 = solid angle = solid angle
|
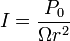 |
| Radiation Momentum, Total Absorption (Inelastic) | 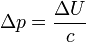 | |
| Radiation Momentum, Total Reflection (Elastic) | 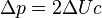 | |
| Radiation Pressure, Total Absorption (Inelastic) | 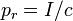 | |
| Radiation Pressure, Total Reflection (Elastic) | 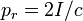 | |
| Intensity Unpolarized Light | 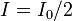 | |
| Malus' Law, Plane Polarized Light | 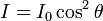 | |
| Brewster's Law of Total
Reflective Polarisation, Brewster's Angle |
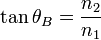 | |
Diffraction/Interferance
Diffraction
| Path Length Difference | 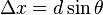 |
| Diffraction Grating Equation | 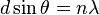
Minima
|
| Diffraction Grating Half-Width | 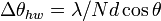 |
| Diffraction Grating Dispersion | 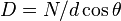 |
| Diffraction Grating resolving power | 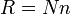 |
| X-Ray Molecular Lattice
Diffraction, Bragg's law, Lattice Distance |
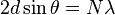 |
| Double-Slit Interference Intensity | 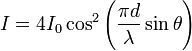 |
| Thin-Film Optics | Air Minima
Air Maxima
|
| Single-Slit Intensity | 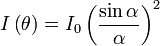 |
| Double Slit Intensity | 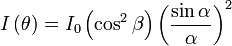
|
| Multiple-Slit Intensity | ![I \left ( \theta \right ) = I_0 \left [ \dfrac{\sin \left ( \dfrac{N \pi a }{\lambda} \sin\theta \right ) }{ \sin \left ( \dfrac{\pi a }{\lambda} \sin\theta \right ) } \right ]^2\,\!](../I/m/00a365025081e9c8208af006cc1b59ff.png) |
| Circular Aperture First Minimum | 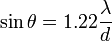 |
| Rayleigh's Criterion | 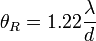 |
External Links
Poynting Vector
EM Waves
Photometry
Radiometry
Interferometry
Referances
- ↑ Essential Principles of Physics, M.J. Hodgson and P.M. Whelan, John Murray 2nd Edition, 1978, ISBN 0-7195-3382-1
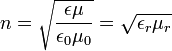
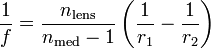
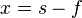
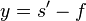
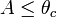
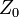 = Impedance of Free Space
= Impedance of Free Space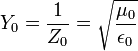
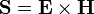
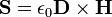
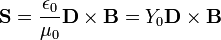
 = position from source
= position from source