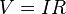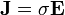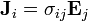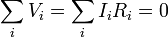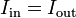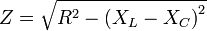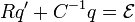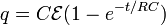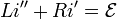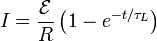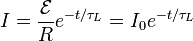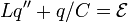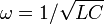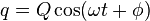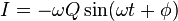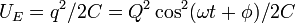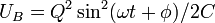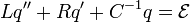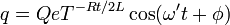Physics Formulae/Electric Circuits Formulae

< Physics Formulae

Lead Article: Tables of Physics Formulae


This article is a summary of the laws, principles, defining quantities, and useful formulae in the analysis of Electric Circuits, Electronics.

DC Quantities

Quantity (Common Name/s) (Common) Symbol/s Defining Equation SI Units Dimension
Electrical Resistance 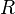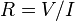R \,\! R = V/I \,\! Ω = V A-1 = J s C-2 [M][L]2 [T]-3 [I]-2
Resistivity, Scalar 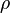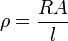\rho \,\! \rho = \frac{RA}{l} \,\! Ω m [M]2 [L]2 [T]-3 [I]-2
Resistivity Temperature Coefficient,

Linear Temperature Dependance

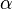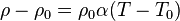 \alpha\,\! \rho - \rho_0 = \rho_0\alpha(T-T_0)\,\! K-1 [Θ]-1
Terminal Voltage for

Power Supply

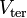 V_\mathrm{ter} \,\! V = J C-1 [M] [L]2 [T]-3 [I]-1
Load Voltage for Circuit 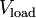V_\mathrm{load} \,\! V = J C-1 [M] [L]2 [T]-3 [I]-1
Internal Resistance of

Power Supply

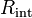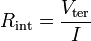 R_\mathrm{int} \,\! R_\mathrm{int} = \frac{V_\mathrm{ter}}{I} \,\! Ω = V A-1 = J s C-2 [M][L]2 [T]-3 [I]-2
Load Resistance of

Circuit

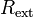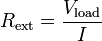 R_\mathrm{ext} \,\! R_\mathrm{ext} = \frac{V_\mathrm{load}}{I} \,\! Ω = V A-1 = J s C-2 [M][L]2 [T]-3 [I]-2
Electromotive Force (emf), Voltage across

entire circuit including power supply, external

components and conductors

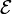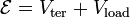 \mathcal{E} \,\! \mathcal{E} = V_\mathrm{ter} + V_\mathrm{load} \,\! V = J C-1 [M] [L]2 [T]-3 [I]-1
Electrical Conductance 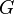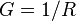G \,\! G = 1/R \,\! S = Ω-1 [T]3 [I]2 [M]-1 [L]-2
Electrical Conductivity, Scalar 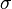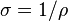\sigma \,\! \sigma = 1/\rho \,\! Ω-1 m-1 [I]2 [T]3 [M]-2 [L]-2
Electrical Conductivity, Tensor 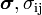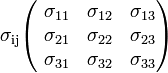\boldsymbol{\sigma}, \sigma_\mathrm{ij} \,\! \sigma_\mathrm{ij} \begin{pmatrix} \ \sigma_{11} & \sigma_{12} & \sigma_{13} \\ \ \sigma_{21} & \sigma_{22} & \sigma_{23} \\ \ \sigma_{31} & \sigma_{32} & \sigma_{33} \end{pmatrix} \,\! Ω-1 m-1 [I]2 [T]3 [M]-2 [L]-2
Electrical Power 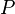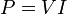P \,\! P=VI\,\! W = J s-1 [M] [L]2 [T]-3
emf Power 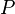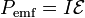P \,\! P_\mathrm{emf} = I\mathcal{E}\,\! W = J s-1 [M] [L]2 [T]-3
Resistor Power Dissipation 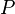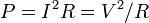P \,\! P = I^2 R = V^2/R \,\! W = J s-1 [M] [L]2 [T]-3
Resistors in Series 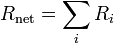R_\mathrm{net} = \sum_i R_i\,\!
Resistors in Parallel 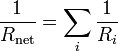\frac{1}{R_\mathrm{net}} = \sum_i \frac{1}{R_i}\,\!
Ohm's Law Scalar form

V=IR \,\!

Vector Form

\mathbf{J} = \sigma \mathbf{E}\,\!

Tensor Form, general applies to all points in a conductor

\mathbf{J}_{i} = \sigma_{ij} \mathbf{E}_{j} \,\!

Kirchoff's Laws emf loop rule around any closed circuit

\sum_i V_i = \sum_i I_i R_i = 0 \,\!

Current law at junctions

I_\mathrm{in} = I_\mathrm{out} \,\!

AC Quantitites

Quantity (Common Name/s) Common Name/s Quantity (Common Name/s) Quantity (Common Name/s) Quantity (Common Name/s)
Resistive Load Voltage 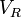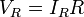V_R \,\! V_R = I_R R \,\! V = J C-1 [M] [L]2 [T]-3 [I]-1
Capacitive Load Voltage 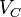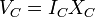V_C \,\! V_C = I_C X_C\,\! V = J C-1 [M] [L]2 [T]-3 [I]-1
Inductive Load Voltage 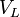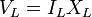V_L \,\! V_L = I_L X_L\,\! V = J C-1 [M] [L]2 [T]-3 [I]-1
Capacitive Reactance 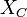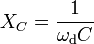X_C \,\! X_C = \frac{1}{\omega_\mathrm{d} C} \,\! Ω-1 m-1 [I]2 [T]3 [M]-2 [L]-2
Inductive Reactance 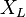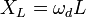X_L \,\! X_L = \omega_d L \,\! Ω-1 m-1 [I]2 [T]3 [M]-2 [L]-2
AC Impedance 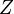Z\,\! V = I Z\,\!

Z = \sqrt{R^2 - \left ( X_L - X_C \right )^2 } \,\!

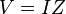
 Ω-1 m-1 [I]2 [T]3 [M]-2 [L]-2
Phase Constant 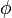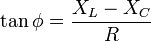\phi \,\! \tan\phi= \frac{X_L - X_C}{R}\,\! dimensionless dimensionless
AC Circuit Resonant

Pulsatance

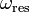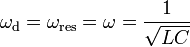 \omega_\mathrm{res} \,\! \omega_\mathrm{d} = \omega_\mathrm{res} = \omega = \frac{1}{\sqrt{LC}}\,\! s-1 [T]-1
AC Peak Current 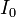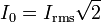I_0 \,\! I_0 = I_\mathrm{rms} \sqrt{2}\,\! A [I]
AC Root Mean

Square Current

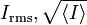 I_\mathrm{rms}, \sqrt{\langle I \rangle} \,\! I_\mathrm{rms} = \sqrt{\frac{1}{T} \int_{0}^{T} \left [ I \left ( t \right ) \right ]^2 \mathrm{d} t} \,\! A [I]
AC Peak Voltage 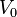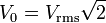V_0 \,\! V_0 = V_\mathrm{rms} \sqrt{2} \,\! V = J C-1 [M] [L]2 [T]-3 [I]-1
AC Root Mean

Square Voltage

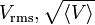 V_\mathrm{rms}, \sqrt{\langle V \rangle} \,\! V_\mathrm{rms} = \sqrt{\frac{1}{T} \int_{0}^{T} \left [ V \left ( t \right ) \right ]^2 \mathrm{d} t} \,\! V = J C-1 [M] [L]2 [T]-3 [I]-1
AC emf, Root Mean Square 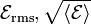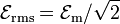\mathcal{E}_\mathrm{rms}, \sqrt{\langle \mathcal{E} \rangle} \,\! \mathcal{E}_\mathrm{rms}=\mathcal{E}_\mathrm{m}/\sqrt{2}\,\! V = J C-1 [M] [L]2 [T]-3 [I]-1
AC Average Power 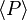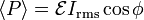\langle P \rangle \,\! \langle P \rangle =\mathcal{E}I_\mathrm{rms}\cos\phi\,\! W = J s-1 [M] [L]2 [T]-3
Capacitive Time Constant 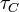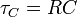\tau_C \,\! \tau_C = RC\,\! s [T]
Inductive Time Constant 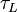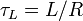\tau_L \,\! \tau_L = L/R\,\! s [T]
RC Circuits RC Circuit Equation

Rq' + C^{-1}q=\mathcal{E}\,\!

RC Circuit Capacitor Charging

q = C\mathcal{E}(1-e^{-t/RC})\,\!

RL Circuits RL Circuit Equation

Li''+Ri'=\mathcal{E}\,\!

RL Circuit Current Rise

I = \frac{\mathcal{E}}{R}\left ( 1-e^{-t/\tau_L}\right )\,\!

RL Circuit, Current Fall

I=\frac{\mathcal{E}}{R}e^{-t/\tau_L}=I_0e^{-t/\tau_L}\,\!

LC Circuit LC Circuit Equation

Lq''+ q/C = \mathcal{E}\,\!

LC Circuit Resonance

\omega = 1/\sqrt{LC}\,\!

LC Circuit Charge

q = Q \cos(\omega t + \phi)\,\!

LC Circuit Current

I=-\omega Q \sin(\omega t + \phi)\,\!

LC Circuit electrical potential energy

U_E=q^2/2C=Q^2\cos^2(\omega t + \phi)/2C\,\!

LC circuit magnetic potential energy

U_B=Q^2\sin^2(\omega t + \phi)/2C\,\!

RLC Circuits RLC Circuit Equation

Lq'' + Rq' +C^{-1}q = \mathcal{E} \,\!

RLC Circuit Charge

q = QeT^{-Rt/2L}\cos(\omega't+\phi)\,\!

This article is issued from Wikiversity - version of the Friday, July 17, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.