Physics Formulae/Conservation and Continuity Equations
< Physics FormulaeLead Article: Tables of Physics Formulae
This article is a summary of the laws, principles, defining quantities, and useful formulae in the analysis of Continuity and Conservation Equations.
To summarize essentails of physics, this section enumerates the classical conservation laws and continuity equations. All the following conservation laws carry through to modern physics, such as Quantum Mechanics, Relativity, Particle Physics and Quantum Relativity, though modifications to conserved quantities may be neccesary. Particle physics introduces new conservation laws, many in a different way using quantum numbers.
For any isolated system (i.e. independant of external agents/influences) the following laws apply to the whole system. Constituents of the system possesing these quantities may experiance changes, but the total amount of the quantity due to all constituents is constant.
Two equivalent ways of applying these in problems is by considering the quantities before and after an event, or considereing any two points in space and time, and equating the initial state of the sytem to the final, since the quantity is conserved.
Corresponding to conserved quantities are currents, current densities, or other time derivatives. These quantites must be conserved also since the amount of a conserved quantity associated with a system is invariant in space and time.
Classical Conservation
| Conserved Quantity | Constancy Equation | System Equation/s | Time Derivatives |
|---|---|---|---|
| Mass | 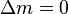 | 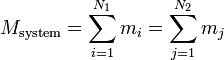 |
Mass current conservation
|
| Linear Momentum | 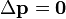 |
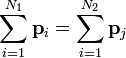
which can be written in equivalant ways, most useful forms are:
|
Momentum current conservation
Momentum current density conservation
|
| Total Angular Momentum | 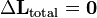 | 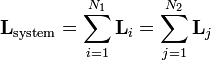
which can be written in equivalant ways, most useful forms are:
|
No analogue |
| Spin Angular Momentum | 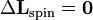 | Same as above | |
| Orbital Angular Momentum | 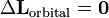 | Same as above | |
| Energy | 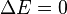 | 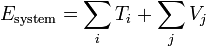
or simply
|
Power conservation
Intensity conservation
|
| Charge | 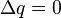 | 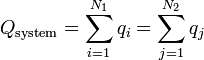 |
Electric current conservation
Electric current density conservation
|
Classical Continuity Equations
Continuity equations describe transport of conserved quantities though a local region of space. Note that these equations are not fundamental simply because of conservation; they can be derived.
| Continuity Description | Nomenclature | General Equation | Simple Case |
|---|---|---|---|
| Hydrodynamics, Fluid Flow | 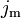 = Mass current current at the cross-section = Mass current current at the cross-section
|
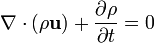 | 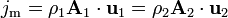 |
| Electromagnetism, Charge | 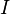 = Electric current at the cross-section = Electric current at the cross-section
|
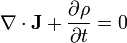 |
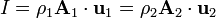 |
| Quantum Mechnics, Probability | 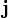 = probablility current/flux = probablility current/flux
|
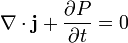 | |
External Links
Conservation Laws
Continiuity Equations
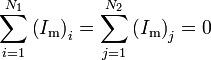
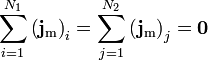
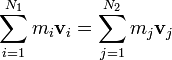
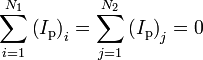
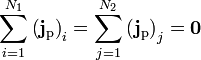
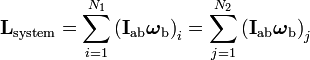
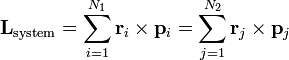
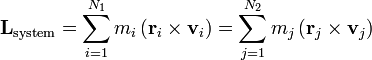
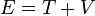
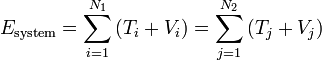
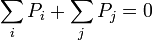
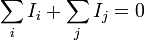
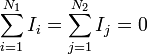
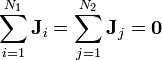
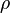 = Volume mass density
= Volume mass density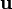 = velocity field of fluid
= velocity field of fluid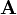 = cross-section
= cross-section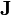 = Electric current density
= Electric current density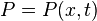 = probablility density function
= probablility density function