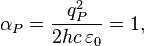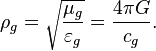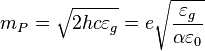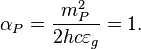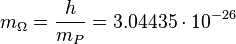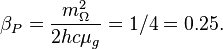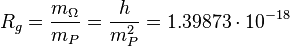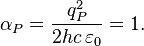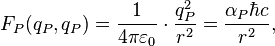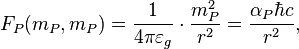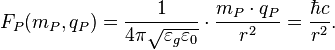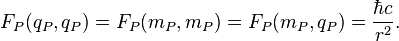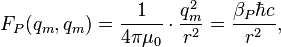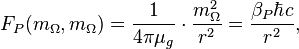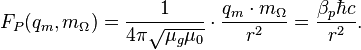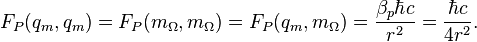Physics/Essays/Fedosin/Planck scale

< Physics < Essays < Fedosin

In physics, Planck scale is the fundamental scale, named after the German physicist Max Planck, who first proposed the ‘’Planck mass’’ in 1899. The electric coupling constant at the Planck scale equals to 1:

\alpha_{P} = \frac{q_P^2}{2hc\,\varepsilon_0} = 1, \

where

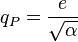$q_P = \frac{e}{\sqrt{\alpha}}$ is the Planck charge;
$\!e$ is the elementary charge;
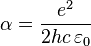$\alpha = \frac{e^2}{2hc\,\varepsilon_0} \$ is the fine structure constant;
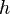$\!h$ is the Planck constant;
$\!c$ is the speed of light in vacuum;
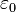$\!\varepsilon_0$ is the vacuum permittivity.

History

The natural units began in 1881, when George Johnstone Stoney derived units of length, time, and mass, now named Stoney units in his honor, by normalizing G, c, and the elementary charge e to 1. (Stoney was also the first to hypothesize that electric charge is quantized and hence to see the fundamental character of e.) Max Planck first set out the base units (q_P excepted) later named in his honor, in a paper presented to the Prussian Academy of Sciences in May 1899.^[1]^[2] That paper also includes the first appearance of the Planck constant named b, and later called h and named after him. The paper gave numerical values for the base units, in terms of the metric system of his day, that were remarkably close to modern values. We are not sure just how Planck came to discover these units because his paper gave no algebraic details. But he did explain why he valued these units as follows:

...ihre Bedeutung fur alle Zeiten und fur alle, auch au?erirdische und au?ermenschliche Kulturen notwendig behalten und welche daher als »naturliche Ma?einheiten« bezeichnet werden konnen...
...These necessarily retain their meaning for all times and for all civilizations, even extraterrestrial and non-human ones, and can therefore be designated as "natural units"...

Fundamental units of vacuum

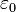The set of primary vacuum constants is: ^[3] the speed of light $~c$ ; the vacuum permittivity $~\varepsilon_0$ ; the speed of gravity 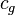$~c_g$ (usually equated to the speed of light); the gravitational constant $~G$ .

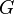The set of secondary vacuum constants is: The vacuum permeability: 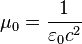$\mu_0 = \frac{1}{\varepsilon_0 c^2}\$ ;

The electromagnetic impedance of free space:

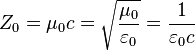Z_0 = \mu_0 c = \sqrt{\frac{\mu_0}{\varepsilon_0}}= \frac{1}{\varepsilon_0 c}

;

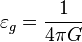The gravitoelectric gravitational constant: $~\varepsilon_g = \frac{1}{4\pi G }$ ;

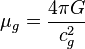The gravitomagnetic gravitational constant: $~\mu_g = \frac{4\pi G }{ c^2_g}$ ;

The gravitational characteristic impedance of free space:

~\rho_g =\sqrt{\frac{\mu_g}{\varepsilon_g}} = \frac{4\pi G }{c_g}.

The above fundamental constants define naturally the following relationship between mass and electric charge:

m_P = \sqrt{2hc\varepsilon_g} = e\sqrt{\frac{\varepsilon_g} {\alpha \varepsilon_0}} \

and these values are the base units of the Planck scale.

Primary Planck units

Gravitational Planck units

Planck mass:

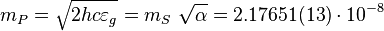m_P = \sqrt{2hc\varepsilon_g} = m_S\ \sqrt{\alpha} = 2.17651(13)\cdot 10^{-8} \

kg,

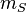where $m_S \$ is the Stoney mass.

Planck gravitational coupling constant:

\alpha_P = \frac{m_P^2}{2hc\varepsilon_g} = 1. \

Planck fictitious gravitational torsion mass:

m_{\Omega} = \frac{h}{m_P} = 3.04435\cdot 10^{-26} \

J s kg⁻¹.

Planck scale gravitational torsion coupling constant: ^[4]

\beta_P = \frac{ m_{\Omega}^2}{2hc\mu_g} = 1/4 = 0.25 . \

Planck gravitational impedance quantum:

R_g = \frac{ m_{\Omega}}{m_P} = \frac{h}{m_P^2} = 1.39873\cdot 10^{-18} \

J s kg⁻².

Electromagnetic Planck units

Planck charge:

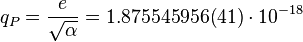q_P = \frac{e}{\sqrt{\alpha}} = 1.875545956(41) \cdot 10^{-18} \

Planck electric coupling constant:

\alpha_P = \frac{q_P^2}{2hc\,\varepsilon_0} = 1. \

Planck fictitious magnetic charge:

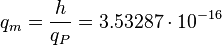q_m = \frac{h}{q_P} = 3.53287\cdot 10^{-16} \

Wb.

Planck scale magnetic coupling constant:

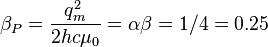\beta_P = \frac{ q_m ^2}{2hc\mu_0} =\alpha \beta = 1/4 = 0.25 \

where 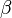$\beta \$ is the magnetic coupling constant.

Planck electrodynamic impedance quantum:

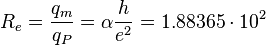R_e = \frac{ q_m }{q_P} = \alpha \frac{h}{e^2} = 1.88365\cdot 10^2 \

Ohm.

Secondary Planck scale units

All systems of measurement feature is base units: in the International System of Units (SI), for example, the base unit of length is the meter. In the system of Planck units, the Planck base unit of length is known simply as the ‘’ Planck length’’, the base unit of time is the ‘’ Planck time’’, and so on. These units are derived from the presented above primary Planck units, and arranged in Table 1 so as to cancel out the unwanted dimensions, leaving only the dimension appropriate to each unit. (Like all systems of natural units, Planck units are an instance of dimensional analysis.)

The keys which are used in the Tables below: L = length, T = time, M = mass, Q = electric charge, Θ = temperature.

Table 1: Secondary Planck units
Name	Dimension	Expressions	SI equivalent ^[3]
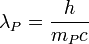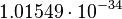Planck wavelength	Length (L)	$\lambda_P = \frac{h}{m_Pc}$	$1.01549\cdot 10^{-34}$ m
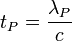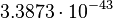Planck time	Time (T)	$t_P = \frac{\lambda_P}{c}$	$3.3873\cdot 10^{-43}$ s
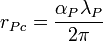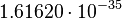Planck classical radius	Length (L)	$r_{Pc} = \frac{\alpha_P \lambda_P}{2\pi}$	$1.61620\cdot 10^{-35}$ m
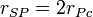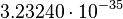Planck Schwarzschild radius	Length (L)	$r_{SP} = 2r_{Pc} \$	$3.23240\cdot 10^{-35}$ m
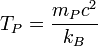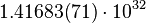Planck temperature	Temperature (Θ)	$T_P = \frac{m_P c^2}{k_B}$	$1.41683(71)\cdot 10^{32}$ K

Planck scale forces

Planck scale static forces

Electric Planck scale force:

F_P(q_P, q_P) = \frac{1}{4\pi \varepsilon_0}\cdot \frac{q_P^2}{r^2} = \frac{\alpha_P \hbar c}{r^2}, \

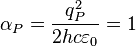where $\alpha_P = \frac{q_P^2}{2h c \varepsilon_0} = 1 \$ is the Planck electric coupling constant.

Gravity Planck scale force:

F_P(m_P, m_P) = \frac{1}{4\pi \varepsilon_g}\cdot \frac{m_P^2}{r^2} = \frac{\alpha_P \hbar c}{r^2}, \

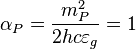where $\alpha_P = \frac{m_P^2}{2hc \varepsilon_g} = 1 \$ is the Planck gravitational coupling constant.

Mixed (charge-mass interaction) Planck force:

F_P(m_P, q_P) = \frac{1}{4\pi \sqrt{\varepsilon_g \varepsilon_0}}\cdot \frac{m_P \cdot q_P}{r^2} = \frac{\hbar c}{r^2}. \

So, at the Planck scale we have the equality of all static forces which describes interactions between charges and masses:

F_P(q_P, q_P) = F_P(m_P, m_P) = F_P(m_P, q_P) = \frac{\hbar c}{r^2}. \

Planck scale dynamic forces

Magnetic Planck scale force:

F_P(q_m, q_m) = \frac{1}{4\pi \mu_0}\cdot \frac{ q_m ^2}{r^2} = \frac{\beta_P \hbar c}{r^2}, \

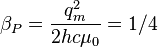where $\beta_P = \frac{ q_m ^2}{2hc\mu_0} = 1/4 \$ is the magnetic Planck coupling constant.

Gravitational torsion force:

F_P(m_{\Omega}, m_{\Omega}) = \frac{1}{4\pi \mu_g}\cdot \frac{ m_{\Omega}^2}{r^2} = \frac{\beta_P\hbar c}{r^2}, \

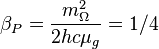where $\beta_P = \frac{ m_{\Omega}^2}{2hc\mu_g} = 1/4 \$ is the Planck gravitational torsion coupling constant.

Mixed dynamic (charge-mass interaction) force:

F_P(q_m, m_{\Omega}) = \frac{1}{4\pi \sqrt{\mu_g \mu_0}}\cdot \frac{ q_m \cdot m_{\Omega}}{r^2} = \frac{\beta_p \hbar c}{r^2}. \

So, at the Planck scale we have the equality of all dynamic forces which describes interactions between dynamic charges and masses:

F_P(q_m, q_m) = F_P(m_{\Omega}, m_{\Omega}) = F_P(q_m, m_{\Omega}) = \frac{\beta_p \hbar c}{r^2} = \frac{\hbar c}{4r^2}. \

References

↑ Planck (1899), p. 479.
↑ Tomilin, K. A., 1999, "Natural Systems of Units: To the Centenary Anniversary of the Planck System," 287-96.
↑ 3.0 3.1 Latest (2010) values of the constants
↑ Yakymakha O.L.(1989). High Temperature Quantum Galvanomagnetic Effects in the Two- Dimensional Inversion Layers of MOSFET's (In Russian). Kyiv: Vyscha Shkola. p.91. ISBN 5-11-002309-3. djvu.

Sources

Planck, Max (1899). "Uber irreversible Strahlungsvorgange". Sitzungsberichte der Koniglich Preu?ischen Akademie der Wissenschaften zu Berlin 5: 440–480. http://bibliothek.bbaw.de/bibliothek-digital/digitalequellen/schriften/anzeige/index_html?band=10-sitz/1899-1&seite:int=454. Pp. 478-80 contain the first appearance of the Planck base units other than the Planck charge, and of Planck's constant, which Planck denoted by b. a and f in this paper correspond to k and G in this entry.

This article is issued from Wikiversity - version of the Thursday, November 06, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.