Order of Operations

In Algebra, the Order of Operations is the sequence to be taken in solving or simplifying equations.

In its simplest form, the order is:

Raising exponents to their powers and extracting roots in the order that you come to them in the problem.
Multiplying and dividing in the order that you come to them in the problem.
Adding and subtracting in the order that you come to them in the problem.

It gets a little more complicated when the problem contains brackets or parentheses, as we must first apply the same order to math inside them before working on the math outside of them.

Examples

Applying the Order of Operations, we would simplify the following expression like this:
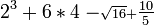
$2^3 + 6 * 4 - \scriptstyle \sqrt{16} + \tfrac{10}{5}$

First, we do the exponents and extra the roots

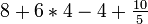
$8 + 6 * 4 - 4 + \tfrac{10}{5}$

Next, we do multiplication and division

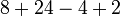
$8 + 24 - 4 + 2$

Finally, we do addition and subtraction

$30$

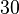
Let's bring the expression above into a new example with parentheses:
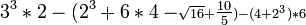
$3^3 * 2 - (2^3 + 6 * 4 - \scriptstyle \sqrt{16} + \tfrac{10}{5}) - (4 + 2^3) * 6$

First, we do exponents and extract roots within the parentheses.

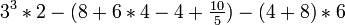
$3^3 * 2 - (8 + 6 * 4 - 4 + \tfrac{10}{5}) - (4 + 8) * 6$

Next, we do multiplication and division within the parentheses.

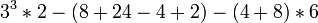
$3^3 * 2 - (8 + 24 - 4 + 2) - (4 + 8) * 6$

Then, we do addition and subtraction within the parentheses.

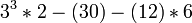
$3^3 * 2 - (30) - (12) * 6$

Now that the parentheses are finished, we do the same thing step by step in the rest of the problem. Exponents & roots:

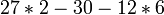
$27 * 2 - 30 - 12 * 6$

Multiplication & division:

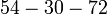
$54 - 30 - 72$

Addition & substraction:

$-48$

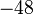
This article is issued from Wikiversity - version of the Sunday, October 17, 2010. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.