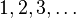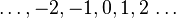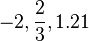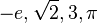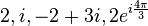Notations

Notations may be a series or system of written symbols used to represent numbers, amounts, or elements in something such as music or mathematics.

Astronomy

Notation: let the symbol \oplus indicate the Earth.

Notation: let the symbol ʘ or \odot indicate the Sun.

Notation: let the symbol I_{\odot} indicate the total solar irradiance.

Notation: let the symbol 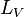L_V indicate the solar visible luminosity.

Notation: let the symbol 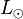L_{\odot} indicate the solar bolometric luminosity.

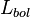Notation: let the symbol L_{bol} indicate the solar bolometric luminosity.

Notation: let the symbol 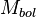M_{bol} represent the bolometric magnitude, the total energy output.

Notation: let the symbol 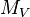M_V represent the visual magnitude.

Notation: let the symbol 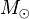M_{\odot} indicate the solar mass.

Notation: let the symbol 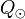Q_{\odot} represent the net solar charge.

Notation: let the symbol 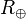R_\oplus indicate the Earth's radius.

Notation: let the symbol 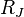R_J indicate the radius of Jupiter.

Notation: let the symbol 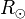R_{\odot} indicate the solar radius.

Semantics

Notation: let the symbol Def. indicate that a definition is following.

Pragmatics

Notation: let the symbols between [ and ] be replacement for that portion of a quoted text.

Notation: let the symbol ... indicate unneeded portion of a quoted text.

Sometimes these are combined as [...] to indicate that text has been replaced by ....

Theoretical notations

Notational locations
Weight Oversymbol Exponent
Coefficient Variable Operation
Number Range Index

For each of the notational locations around the central Variable, conventions are often set by consensus as to use. For example, Exponent is often used as an exponent to a number or variable: 2-2 or x2.

In the Notations at the top of this section, Index is replaced by symbols for the Sun (ʘ), Earth (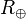R_\oplus), or can be for Jupiter (J) such as R_J.

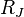A common Oversymbol is one for the average 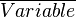\overline{Variable}.

Operation may be replaced by a function, for example.

All notational locations could look something like

bx - x = n
a 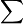\sum f(x)
n → ∞

where the center line means "a x Σ f(x)" for all added up values of f(x) when x = n from say 0 to infinity with each term in the sum before summation multiplied by bn, then divided by n for an average whenever n is finite.

Mathematics

1, 2, 3,\ldots\! \ldots,-2, -1, 0, 1, 2\,\ldots\! -2, \frac{2}{3}, 1.21\,\! -e, \sqrt{2}, 3, \pi\,\! 2, i, -2+3i, 2e^{i\frac{4\pi}{3}}\,\!
Natural numbers Integers Rational numbers Real numbers Complex numbers
A calculator display showing an approximation to the Avogadro constant in E notation. Credit: PRHaney.

Sciences

"Scientific notation (more commonly known as standard form) is a way of writing numbers that are too big or too small to be conveniently written in decimal form. Scientific notation has a number of useful properties and is commonly used in calculators and by scientists, mathematicians and engineers."[1]

Standard decimal notation Normalized scientific notation
2 2×100
300 3×102
4,321.768 4.321768×103
-53,000 −5.3×104
6,720,000,000 6.72×109
0.2 2×10−1
0.000 000 007 51 7.51×10−9

"A metric prefix or SI prefix is a unit prefix that precedes a basic unit of measure to indicate a decadic multiple or fraction of the unit. Each prefix has a unique symbol that is prepended to the unit symbol."[2]

Metric prefixes
Prefix Symbol 1000m 10n Decimal Short scale Long scale Since[n 1]
yotta Y 10008 1024 1000000000000000000000000 septillion quadrillion 1991
zetta Z 10007 1021 1000000000000000000000 sextillion trilliard 1991
exa E 10006 1018 1000000000000000000 quintillion trillion 1975
peta P 10005 1015 1000000000000000 quadrillion billiard 1975
tera T 10004 1012 1000000000000 trillion billion 1960
giga G 10003 109 1000000000 billion milliard 1960
mega M 10002 106 1000000 million 1960
kilo k 10001 103 1000 thousand 1795
hecto h 10002/3 102 100 hundred 1795
deca da 10001/3 101 10 ten 1795
10000 100 1 one –
deci d 1000−1/3 10−1 0.1 tenth 1795
centi c 1000−2/3 10−2 0.01 hundredth 1795
milli m 1000−1 10−3 0.001 thousandth 1795
micro μ 1000−2 10−6 0.000001 millionth 1960
nano n 1000−3 10−9 0.000000001 billionth milliardth 1960
pico p 1000−4 10−12 0.000000000001 trillionth billionth 1960
femto f 1000−5 10−15 0.000000000000001 quadrillionth billiardth 1964
atto a 1000−6 10−18 0.000000000000000001 quintillionth trillionth 1964
zepto z 1000−7 10−21 0.000000000000000000001 sextillionth trilliardth 1991
yocto y 1000−8 10−24 0.000000000000000000000001 septillionth quadrillionth 1991
  1. ↑ The metric system was introduced in 1795 with six prefixes. The other dates relate to recognition by a resolution of the General Conference on Weights and Measures (CGPM)]].

Research

Hypothesis:

  1. Ancient languages may have been little more than notations.

Control groups

This is an image of a Lewis rat. Credit: Charles River Laboratories.

The findings demonstrate a statistically systematic change from the status quo or the control group.

“In the design of experiments, treatments [or special properties or characteristics] are applied to [or observed in] experimental units in the treatment group(s).[3] In comparative experiments, members of the complementary group, the control group, receive either no treatment or a standard treatment.[4]"[5]

Proof of concept

Def. a “short and/or incomplete realization of a certain method or idea to demonstrate its feasibility"[6] is called a proof of concept.

Def. evidence that demonstrates that a concept is possible is called proof of concept.

The proof-of-concept structure consists of

  1. background,
  2. procedures,
  3. findings, and
  4. interpretation.[7]

See also

References

  1. ↑ "Scientific notation, In: Wikipedia". San Francisco, California: Wikimedia Foundation, Inc. January 25, 2013. Retrieved 2013-01-30.
  2. ↑ "Metric prefix, In: Wikipedia". San Francisco, California: Wikimedia Foundation, Inc. January 21, 2013. Retrieved 2013-02-01.
  3. ↑ Klaus Hinkelmann, Oscar Kempthorne (2008). Design and Analysis of Experiments, Volume I: Introduction to Experimental Design (2nd ed.). Wiley. ISBN 978-0-471-72756-9. http://books.google.com/?id=T3wWj2kVYZgC&printsec=frontcover.
  4. ↑ R. A. Bailey (2008). Design of comparative experiments. Cambridge University Press. ISBN 978-0-521-68357-9. http://www.cambridge.org/uk/catalogue/catalogue.asp?isbn=9780521683579.
  5. ↑ "Treatment and control groups, In: Wikipedia". San Francisco, California: Wikimedia Foundation, Inc. May 18, 2012. Retrieved 2012-05-31.
  6. ↑ "proof of concept, In: Wiktionary". San Francisco, California: Wikimedia Foundation, Inc. November 10, 2012. Retrieved 2013-01-13.
  7. ↑ Ginger Lehrman and Ian B Hogue, Sarah Palmer, Cheryl Jennings, Celsa A Spina, Ann Wiegand, Alan L Landay, Robert W Coombs, Douglas D Richman, John W Mellors, John M Coffin, Ronald J Bosch, David M Margolis (August 13, 2005). "Depletion of latent HIV-1 infection in vivo: a proof-of-concept study". Lancet 366 (9485): 549-55. doi:10.1016/S0140-6736(05)67098-5. http://www.ncbi.nlm.nih.gov/pmc/articles/PMC1894952/. Retrieved 2012-05-09.

External links

This article is issued from Wikiversity - version of the Friday, February 12, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.