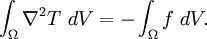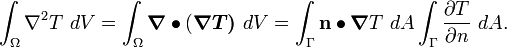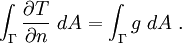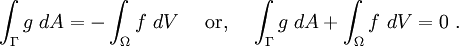Nonlinear finite elements/Weak form of heat equation
< Nonlinear finite elementsWeak Form of the Heat Equation
Let us now derive the weak form of the model of heat conduction in equations (16). It is more convenient to use the form of the governing equation given in equation (10). The equation is
Let 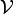 be the space of weighting functions (or test functions). Then
any
be the space of weighting functions (or test functions). Then
any 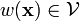 (
(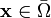 ) is continuously
differentiable. The weighting functions also satisfy
) is continuously
differentiable. The weighting functions also satisfy 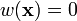 on
on
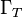 . Recall that we called a similar set of functions
. Recall that we called a similar set of functions 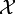 in
our discussion of the Poisson problem. We can write
in
our discussion of the Poisson problem. We can write
Let 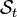 be the set of trial solutions. Then any trial function
be the set of trial solutions. Then any trial function
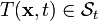 has to satisfy the essential boundary conditions
on
has to satisfy the essential boundary conditions
on 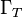 . This is written as
. This is written as
To get the weak form, we multiply the governing equation by the weighting function and integrate over the volume to get
The second term in the equation has second-order derivatives. We will convert these into first order derivatives using the divergence theorem and the identity
From the identity we get
Substitute (29) into the second term in (28) to get
Apply the divergence theorem to the first term on the right hand side of (30). You will get
where 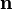 is the unit outward normal to the boundary
is the unit outward normal to the boundary 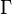 .
.
Since 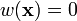 on
on 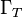 , equation (31) becomes
, equation (31) becomes
Substitute (31) into (30) and (30) back into (28). You will get
After rearrangement, we get the exact weak form of the heat equation
Recall that equation (15) gives us
Therefore equation (34) can be written as
In more compact notation
Following the same process for the initial condition, we get
In compact notation,
The variation initial boundary value problem for heat conduction can then be stated as follows.
Well-Posedness of the Boundary Value Problem
Unless  has a simple geometry - square, spherical or cylindrical,
it is very difficult to solve the BVP in closed form (using separation
of variables, for instance). For some BVPs, it may not be possible
at all to get a closed form solution. In fact, it may not even be
obvious that a solution exists or is unique or that the solution depends
continuously on the data.
has a simple geometry - square, spherical or cylindrical,
it is very difficult to solve the BVP in closed form (using separation
of variables, for instance). For some BVPs, it may not be possible
at all to get a closed form solution. In fact, it may not even be
obvious that a solution exists or is unique or that the solution depends
continuously on the data.
A well-posed problem is one that satisfied the three conditions:
- a solution exists.
- the solution is unique.
- the solution depends continuously on the data (that is, smallchanges in the data do not cause wild fluctuations in the solution).
BVPs can be used to get reliable results only when they are well-posed.
Let us look at an example. Recall the BVP for the Poisson equation.
Assume that 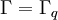 . That means that the heat flux is given on
the entire boundary.
. That means that the heat flux is given on
the entire boundary.
Suppose 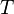 is a solution. Then
is a solution. Then 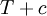 is also a solution, where
is also a solution, where  is a constant. To see why, compute the Laplacian of
is a constant. To see why, compute the Laplacian of 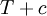 .
.
So the solution 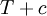 satisfies the PDE.
satisfies the PDE.
How about the boundary conditions?Plug in 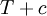 into the boundary
condition to get
into the boundary
condition to get
So the boundary conditions are also satisfied. That means that if
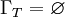 , then the solution is not unique. We can
add any constant temperature to the body and the solution will be consistent
with the governing equations.
, then the solution is not unique. We can
add any constant temperature to the body and the solution will be consistent
with the governing equations.
We can also check the conditions under which a solution will exist for
this problem. Integrate the Poisson equation over  to get
to get
Apply the divergence theorem to the Laplacian. We get
From the boundary condition,
Therefore, we have
The boxed equation is called a compatibility condition and a solution does not exist unless this condition is satisfied.
In the context of the steady heat conduction problem, the compatibility condition says that the heat generated in the body must equal the heat flux. A similar (but more complicated) exercise can be used to show the existence and uniqueness of solutions for the full heat equation.
![\rho~C_v~\frac{\partial T}{\partial t} - \boldsymbol{\nabla} \bullet [\boldsymbol{\kappa}\bullet\boldsymbol{\nabla T]} = s~.](../I/m/2e6708f52b7f744ab16fb30da71d2b72.png)
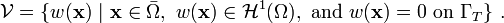
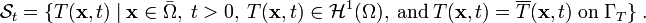
![\text{(28)} \qquad
\int_{\Omega} \left(\rho~C_v~\frac{\partial T}{\partial t}\right)~w~dV -
\int_{\Omega} \left[\boldsymbol{\nabla} \bullet (\boldsymbol{\kappa}\bullet\boldsymbol{\nabla T)}\right]~w~dV =
\int_{\Omega} s~w~dV~.](../I/m/653d744af883caa8599e0da6439eaf9d.png)
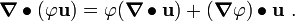
![\text{(29)} \qquad
w\left[\boldsymbol{\nabla} \bullet (\boldsymbol{\kappa}\bullet\boldsymbol{\nabla} T)\right] =
\boldsymbol{\nabla} \bullet \left[w~(\boldsymbol{\kappa}\bullet\boldsymbol{\nabla} T)\right] -
(\boldsymbol{\nabla} w)\bullet(\boldsymbol{\kappa}\bullet\boldsymbol{\nabla} T) ~.](../I/m/d05d0735bfff3555fbde62af16ae8dde.png)
![\text{(30)} \qquad
\int_{\Omega} \left[\boldsymbol{\nabla} \bullet (\boldsymbol{\kappa}\bullet\boldsymbol{\nabla} T)\right]~w~dV =
\int_{\Omega} \boldsymbol{\nabla} \bullet \left[w~(\boldsymbol{\kappa}\bullet\boldsymbol{\nabla} T)\right]~dV
- \int_{\Omega} (\boldsymbol{\nabla} w)\bullet(\boldsymbol{\kappa}\bullet\boldsymbol{\nabla} T)~dV ~.](../I/m/86eef4ee3d8ec0efb234a5e684c06090.png)
![\text{(31)} \qquad
\int_{\Omega} \boldsymbol{\nabla} \bullet \left[w~(\boldsymbol{\kappa}\bullet\boldsymbol{\nabla} T)\right]~dV=
\int_{\Gamma} \left[w~(\boldsymbol{\kappa}\bullet\boldsymbol{\nabla} T)\right]\bullet\mathbf{n}~dA](../I/m/42d52e1e6afbc15fd35dd3ce9beffda4.png)
![\text{(32)} \qquad
\int_{\Omega} \boldsymbol{\nabla} \bullet \left[w~(\boldsymbol{\kappa}\bullet\boldsymbol{\nabla} T)\right]~dV=
\int_{\Gamma_q} \left[w~(\boldsymbol{\kappa}\bullet\boldsymbol{\nabla} T)\right]\bullet\mathbf{n}~dA~.](../I/m/d75a1702e0d545238032c4a597e11c48.png)
![\text{(33)} \qquad
\int_{\Omega} \left(\rho~C_v~\frac{\partial T}{\partial t}\right)~w~dV -
\int_{\Gamma_q} \left[w~(\boldsymbol{\kappa}\bullet\boldsymbol{\nabla} T)\right]\bullet\mathbf{n}~dA
+ \int_{\Omega} (\boldsymbol{\nabla} w)\bullet(\boldsymbol{\kappa}\bullet\boldsymbol{\nabla} T)~dV=
\int_{\Omega} s~w~dV~.](../I/m/6c6da7a9e544ac94cc5b4764a4989ac5.png)
![\text{(34)} \qquad
{
\int_{\Omega} \left(\rho~C_v~\frac{\partial T}{\partial t}\right)~w~dV +
\int_{\Omega} (\boldsymbol{\nabla} w)\bullet(\boldsymbol{\kappa}\bullet\boldsymbol{\nabla} T)~dV=
\int_{\Omega} s~w~dV +
\int_{\Gamma_q} \left[w~(\boldsymbol{\kappa}\bullet\boldsymbol{\nabla} T)\right]\bullet\mathbf{n}~dA~.
}](../I/m/59b5204bdb6da6ed196396b8f0269d96.png)
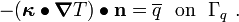
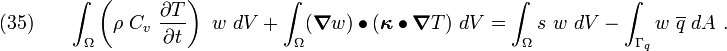
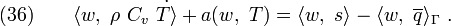
![\text{(37)} \qquad
{
\int_{\Omega} w~\left[\rho~C_v~T(0)\right]~dV =
\int_{\Omega} w~\left[\rho~C_v~T_0\right]~dV ~.
}](../I/m/7d73953dd942112f441cd85dad79fd9b.png)
![{
\begin{align}
& \mathsf{ Variational~ BVP ~for~ the ~Heat~ Equation}\\
& \\
\text{Find a function} & ~T(t) \in \mathcal{S}_t, t \in [0,\tau]
~\text{such that for all}~ w \in \mathcal{V}\\
& \\
& \int_{\Omega} \left(\rho~C_v~\frac{\partial T}{\partial t}\right)~w~dV +
\int_{\Omega} (\boldsymbol{\nabla} w)\bullet(\boldsymbol{\kappa}\bullet\boldsymbol{\nabla} T)~dV=
\int_{\Omega} s~w~dV -
\int_{\Gamma_q} w~\overline{q}~dA \\
& \int_{\Omega} w~\rho~C_v~T(0)~dV =
\int_{\Omega} w~\rho~C_v~T_0~dV ~.
\end{align}
}](../I/m/b0fe48d914e497488d66c68702675187.png)
![\nabla^2 (T+c) = \boldsymbol{\nabla} \bullet [\boldsymbol{\nabla (T+c)]} = \boldsymbol{\nabla} \bullet (\boldsymbol{\nabla T)} = \nabla^2 T~.](../I/m/8e969086eb7bafc961dfb1897b528849.png)
![\frac{\partial (T+c)}{\partial n} = [\boldsymbol{\nabla} (T+c)]\bullet\mathbf{n} = (\boldsymbol{\nabla} T)\bullet\mathbf{n}
= \frac{\partial T}{\partial n}](../I/m/c62ff83558dd60ce1d3aa05b0cd16efa.png)