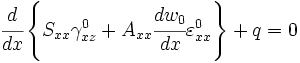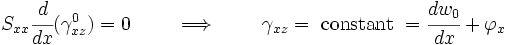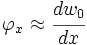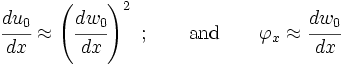Nonlinear finite elements/Timoshenko beams
< Nonlinear finite elementsTimoshenko Beam
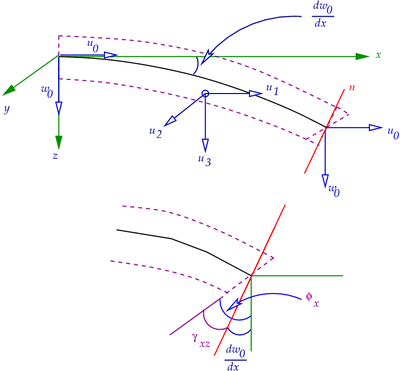 Timoshenko beam. |
Displacements
Strains
Principle of Virtual Work
where
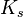 = shear correction factor
= shear correction factor
Taking Variations
Take variation
Take variation
Take variation
Internal Virtual Work
Integrate by Parts
Get rid of derivatives of the variations.
Collect terms
Euler-Lagrange Equations
Constitutive Relations
Then,
where
Equilibrium Equations
Weak Form
Finite element model
Trial Solution
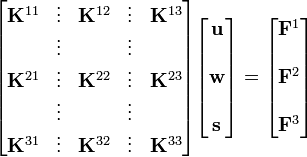
Element Stiffness Matrix
Choice of Approximate Solutions
Choice 1
 = linear (
= linear ( )
) 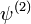 = linear (
= linear (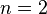 )
)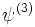 = linear (
= linear (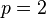 ).
).
Nearly singular stiffness matrix (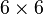 ).
).
Choice 2
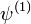 = linear (
= linear (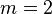 )
) 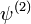 = quadratic (
= quadratic (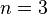 )
)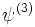 = linear (
= linear (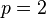 ).
).
The stiffness matrix is (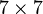 ). We can statically condense out
the interior degree of freedom and get a (
). We can statically condense out
the interior degree of freedom and get a (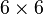 ) matrix.
The element behaves well.
) matrix.
The element behaves well.
Choice 3
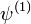 = linear (
= linear (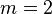 )
) 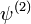 = cubic (
= cubic (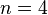 )
)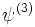 = quadratic (
= quadratic (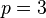 )
)
The stiffness matrix is (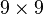 ). We can statically condense out
the interior degrees of freedom and get a (
). We can statically condense out
the interior degrees of freedom and get a (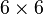 ) matrix.
If the shear and bending stiffnesses are element-wise constant, this
element gives exact results.
) matrix.
If the shear and bending stiffnesses are element-wise constant, this
element gives exact results.
Shear Locking
Example Case
Linear 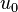 , Linear
, Linear 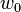 , Linear
, Linear 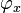 .
.
But, for thin beams,
If constant 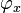
Also
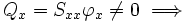 Non-zero transverse shear.
Non-zero transverse shear.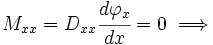 Zero bending energy.
Zero bending energy.
Result: Zero displacements and rotations 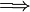 Shear Locking!
Shear Locking!
Recall
or,
If 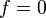 and
and 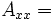 constant
constant
If there is only bending but no stretching,
Hence,
Also recall:
or,
If 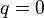 and
and 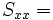 constant, and no membrane strains
constant, and no membrane strains
Hence,
Shape functions need to satisfy:
Example Case 1
Linear 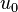 , Linear
, Linear 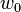 , Linear
, Linear 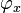 .
.
- First condition
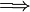 constant
constant  constant. Passes! No Membrane Locking.
constant. Passes! No Membrane Locking. - Second condition
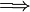 linear
linear  constant. Fails! Shear Locking.
constant. Fails! Shear Locking.
Example Case 2
Linear 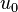 , Quadratic
, Quadratic 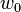 , Linear
, Linear 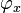 .
.
- First condition
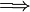 constant
constant  quadratic. Fails! Membrane Locking.
quadratic. Fails! Membrane Locking. - Second condition
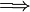 linear
linear  linear. Passes! No Shear Locking.
linear. Passes! No Shear Locking.
Example Case 3
Quadratic 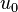 , Quadratic
, Quadratic 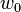 , Linear
, Linear 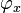 .
.
- First condition
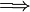 linear
linear  quadratic. Fails! Membrane Locking.
quadratic. Fails! Membrane Locking. - Second condition
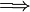 linear
linear  linear. Passes! No Shear Locking.
linear. Passes! No Shear Locking.
Example Case 4
Cubic 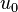 , Quadratic
, Quadratic 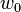 , Linear
, Linear 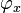 .
.
- First condition
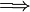 quadratic
quadratic  quadratic. Passes! No Membrane Locking.
quadratic. Passes! No Membrane Locking. - Second condition
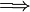 linear
linear  linear. Passes! No Shear Locking.
linear. Passes! No Shear Locking.
Overcoming Shear Locking
Option 1
- Linear
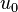 , linear
, linear 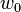 , linear
, linear 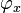 .
. - Equal interpolation for both
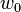 and
and 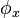 .
. - Reduced integration for terms containing
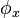 - treat as constant.
- treat as constant.
Option 2
- Cubic
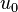 , quadratic
, quadratic 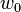 , linear
, linear 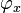 .
. - Stiffness matrix is
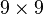 .
. - Hard to implement.
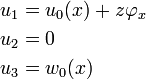
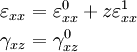
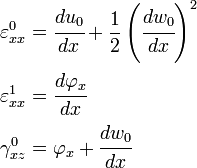
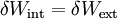
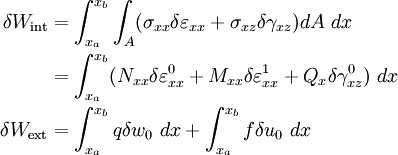
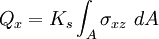
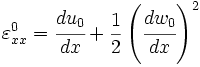
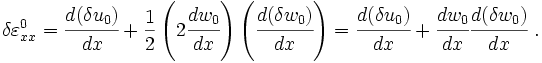
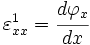
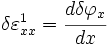
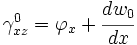
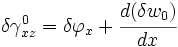
![\begin{align}
\int_{x_a}^{x_b} N_{xx}\delta \varepsilon_{xx}^0~dx & =
\int_{x_a}^{x_b} N_{xx}\left[
\cfrac{d(\delta u_0)}{dx}+\cfrac{dw_0}{dx}\cfrac{d(\delta w_0)}{dx}\right]~dx \\
\int_{x_a}^{x_b} M_{xx}\delta \varepsilon_{xx}^1~dx & =
\int_{x_a}^{x_b} M_{xx}\left[\cfrac{d\delta \varphi_x}{dx}\right]~dx \\
\int_{x_a}^{x_b} Q_{x}\delta \gamma_{xz}^0~dx & =
\int_{x_a}^{x_b} Q_{x} \left[\delta \varphi_x + \cfrac{d(\delta w_0)}{dx}\right]~dx
\end{align}](../I/m/de484d3c8d5a0b8fd238ddef8033bdeb.png)
![\begin{align}
\delta W_{\text{int}} = \int_{x_a}^{x_b} & \left\{ N_{xx}\left[
\cfrac{d(\delta u_0)}{dx}+\cfrac{dw_0}{dx}\cfrac{d(\delta w_0)}{dx}\right]\right.
+ \\
&M_{xx}\left[\cfrac{d\delta \varphi_x}{dx}\right] +
\left.
Q_{x} \left[\delta \varphi_x + \cfrac{d(\delta w_0)}{dx}\right]\right\}~dx
\end{align}](../I/m/287fccef509809d95c2f4efe5a3c4955.png)
![\begin{align}
\int_{x_a}^{x_b} N_{xx}&\left[
\cfrac{d(\delta u_0)}{dx}+\cfrac{dw_0}{dx}\cfrac{d(\delta w_0)}{dx}\right]~dx
= \left[N_{xx}\delta u_0\right]_{x_a}^{x_b} -
\int_{x_a}^{x_b} \cfrac{dN_{xx}}{dx}\delta u_0~dx + \\
& \qquad \qquad \qquad
\left[N_{xx}\cfrac{dw_0}{dx}\delta w_0\right]_{x_a}^{x_b} -
\int_{x_a}^{x_b} \cfrac{d}{dx}\left(N_{xx}\cfrac{dw_0}{dx}\right)\delta w_0~dx \\
\\
\int_{x_a}^{x_b} M_{xx}&\left[\cfrac{d(\delta \varphi_x)}{dx}\right]~dx
= \left[M_{xx}\delta \varphi_x\right]_{x_a}^{x_b} -
\int_{x_a}^{x_b} \cfrac{dM_{xx}}{dx}\delta \varphi_x~dx \\
\\
\int_{x_a}^{x_b} Q_{x} &\left[\delta \varphi_x + \cfrac{d(\delta w_0)}{dx}\right]~dx
= \int_{x_a}^{x_b} Q_{x} \delta \varphi_x~dx +
\left[Q_{x}\delta w_0\right]_{x_a}^{x_b} -
\int_{x_a}^{x_b} \cfrac{dQ_{x}}{dx}\delta w_0~dx
\end{align}](../I/m/4cc87280df428e549d60a7f0675e8d8e.png)
![\begin{align}
&\left[N_{xx}{\delta u_0}\right]_{x_a}^{x_b} -
\int_{x_a}^{x_b} \cfrac{dN_{xx}}{dx}{\delta u_0}~dx + \\
&\left[N_{xx}\cfrac{dw_0}{dx}\delta w_0 +
Q_{x}\delta w_0\right]_{x_a}^{x_b} -
\int_{x_a}^{x_b} \left[\cfrac{d}{dx}\left(N_{xx}\cfrac{dw_0}{dx}\right) +
\cfrac{dQ_{x}}{dx}\right]\delta w_0~dx + \\
&\left[M_{xx}\delta \varphi_x\right]_{x_a}^{x_b} -
\int_{x_a}^{x_b} \left(\cfrac{dM_{xx}}{dx} - Q_x \right)\delta \varphi_x~dx \\
&= \int_{x_a}^{x_b} q~\delta w_0~dx + \int_{x_a}^{x_b} f{\delta u_0}~dx
\end{align}](../I/m/ef2a151c6b32fdcebb22363489e0c07c.png)
![\begin{align}
\int_{x_a}^{x_b} \left(\cfrac{dN_{xx}}{dx} + f\right){\delta u_0}~dx & =
\left[N_{xx}{\delta u_0}\right]_{x_a}^{x_b} \\
\int_{x_a}^{x_b} \left[\cfrac{d}{dx}\left(N_{xx}\cfrac{dw_0}{dx}\right) +
\cfrac{dQ_{x}}{dx} + q \right]~\delta w_0~dx& =
\left[N_{xx}\cfrac{dw_0}{dx}~\delta w_0 +
Q_{x}~\delta w_0\right]_{x_a}^{x_b} \\
\int_{x_a}^{x_b} \left(\cfrac{dM_{xx}}{dx} - Q_x \right)~\delta \varphi_x~dx &=
\left[M_{xx}~\delta \varphi_x\right]_{x_a}^{x_b}
\end{align}](../I/m/7faa953a068a009e3a0d67b32ea85639.png)
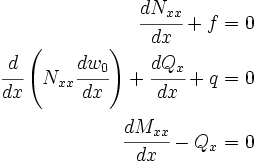

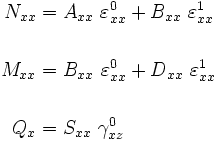
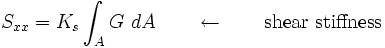
![\begin{align}
\cfrac{d}{dx}\left\{
A_{xx} \left[ \cfrac{du_0}{dx} + \frac{1}{2}\left(\cfrac{dw_0}{dx}\right)^2 \right]
\right\} + f & = 0 \\
\cfrac{d}{dx}\left\{
S_{xx} \left( \cfrac{dw_0}{dx} + \varphi_x \right) +
A_{xx} \cfrac{dw_0}{dx} \left[
\cfrac{du_0}{dx} + \frac{1}{2}\left(\cfrac{dw_0}{dx}\right)^2
\right] \right\} + q & = 0 \\
\cfrac{d}{dx}\left(D_{xx}\cfrac{d\varphi_x}{dx}\right) +
S_{xx}\left( \cfrac{dw_0}{dx} + \varphi_x \right)& = 0
\end{align}](../I/m/b5e83a752c120e69881cc0f3ed305b74.png)
![\begin{align}
\int_{x_a}^{x_b} A_{xx} \cfrac{d(\delta u_0)}{dx}
\left[ \cfrac{du_0}{dx} + \frac{1}{2}\left(\cfrac{dw_0}{dx}\right)^2 \right]~dx &=
\int_{x_a}^{x_b} f\delta u_0~dx + \left[N_{xx}\delta u_0\right]_{x_a}^{x_b} \\
\\
\int_{x_a}^{x_b} A_{xx}\cfrac{d(\delta w_0)}{dx}\cfrac{dw_0}{dx}
\left[ \cfrac{du_0}{dx} + \frac{1}{2}\left(\cfrac{dw_0}{dx}\right)^2 \right]~dx &+
\int_{x_a}^{x_b} S_{xx}\cfrac{d(\delta w_0)}{dx}\left(\cfrac{dw_0}{dx}+\varphi_x\right)~dx
= \\
&\int_{x_a}^{x_b} q\delta u_0~dx +
\left[\left(N_{xx}\cfrac{dw_0}{dx}+Q_x \right)\delta w_0\right]_{x_a}^{x_b} \\
\\
-\int_{x_a}^{x_b} S_{xx}\delta \varphi_x\left(\cfrac{dw_0}{dx}+\varphi_x\right)~dx & +
\int_{x_a}^{x_b} D_{xx}\cfrac{d(\delta \varphi_x)}{dx}\cfrac{d\varphi_x}{dx}~dx=
\left[M_{xx}\delta \varphi_x\right]_{x_a}^{x_b}
\end{align}](../I/m/b9314b9aa155244b0d3dd47cefe99a52.png)
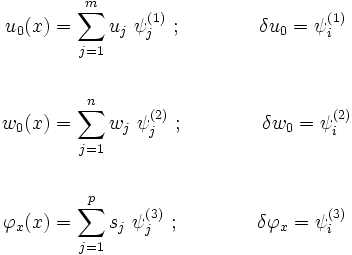
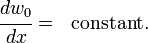
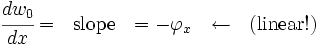
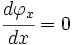
![\cfrac{d}{dx}\left\{
A_{xx} \left[ \cfrac{du_0}{dx} + \frac{1}{2}\left(\cfrac{dw_0}{dx}\right)^2 \right]
\right\} + f= 0](../I/m/9b539f692e8334e28e9f1281f446fed5.png)
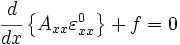
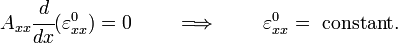
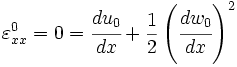
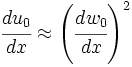
![\cfrac{d}{dx}\left\{
S_{xx} \left( \cfrac{dw_0}{dx} + \varphi_x \right) +
A_{xx} \cfrac{dw_0}{dx} \left[
\cfrac{du_0}{dx} + \frac{1}{2}\left(\cfrac{dw_0}{dx}\right)^2
\right] \right\} + q = 0](../I/m/131b84270603b0ba58dc8084cb407bef.png)