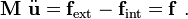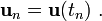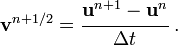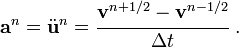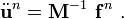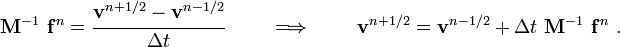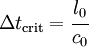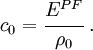Nonlinear finite elements/Solution procedure
< Nonlinear finite elementsSolution Procedure
The finite element system of equations is
Let's assume that the mass matrix is diagonal. Let us also assume that we would like to solve this problem using an explicit method that uses central differencing.
Let the time step size be 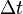 . Let us also assume that the time
step is constant. Then, at time step
. Let us also assume that the time
step is constant. Then, at time step  , the time is
, the time is 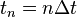 .
.
Let
Let us take a half step to compute the velocity at the middle of the timestep. Then,
We will use this half-step velocity to compute the acceleration
Now,
Therefore,
Algorithm
- Initialize:
- Set
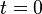 and
and 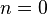 .
. - Set the initial velocities (
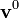 ) at the nodes.
) at the nodes. - Set the initial accelerations (
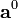 ) at the nodes.
) at the nodes. - Set the initial stresses (
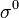 ) at the element Gauss points.
) at the element Gauss points. - Compute the lumped mass
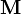 at the nodes.
at the nodes.
- Set
- Set the displacements and velocities at the first time step:
- Displacement:
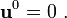
- Velocity:
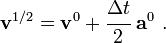
- Displacement:
- Apply essential BCs:
![[\mathbf{v}^{1/2}]_{\Gamma_v} = \bar{\mathbf{v}}(\mathbf{x}, \Delta t/2) ~.](../I/m/d010e75d57d71b911110024841cb1727.png)
- Update the nodal displacements:
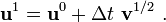
- Set
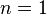 and
and 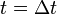 .
. - Loop through the following steps until
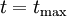 .
. - For each element (at the Gauss points):
- Compute the strain measure:
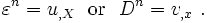
- Compute the stress:
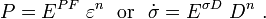
- Compute the strain measure:
- For each node:
- Compute the internal force
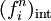 .
. - Compute the external force
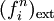 .
. - Compute the total force
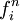 .
. - Compute the acceleration
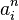 :
: 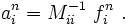
- Update the velocity
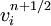 .
. 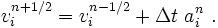
- Apply the essential boundary conditions.
- Update the displacement
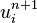 .
. 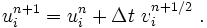
- Compute the internal force
- Update the counters:
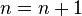 ,
, 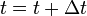 .
.
Stability of the Explicit Algorithm
If the time step 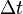 is too large, the algorithm may not be stable
and may give unreasonable results. To provide a check on the time step
size, we use the CFL (Courant-Friedrichs-Lewy) condition to determine
is too large, the algorithm may not be stable
and may give unreasonable results. To provide a check on the time step
size, we use the CFL (Courant-Friedrichs-Lewy) condition to determine
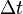 . This condition (in 1-D) states that
. This condition (in 1-D) states that
where 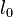 is the initial length of the element, and
is the initial length of the element, and
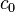 is speed of sound in the material (wavespeed) given by
is speed of sound in the material (wavespeed) given by