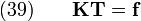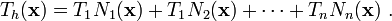Nonlinear finite elements/Solution of Poisson equation
< Nonlinear finite elementsConstruction of Approximate Solutions
If we know that the problem is well-posed but does not have a closed form solution, we can go ahead and try to get an approximate solution. The finite element method is one way of getting at approximate solutions (among many other numerical methods).
The finite element method starts off with the variational form (or the weak form) of the BVP. The method is a special case of a class of methods called Galerkin methods.
Finite element solution for the Poisson equation
Recall the variational boundary value problem for the Poisson equation:
The space 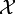 is continuous and an infinite number of functions could
be chosen from this space of functions. In the finite element
method, we choose a trial function from the space of approximate
solutions
is continuous and an infinite number of functions could
be chosen from this space of functions. In the finite element
method, we choose a trial function from the space of approximate
solutions 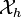 where
where 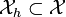 . A defining feature
of these approximate trial solutions is that they are associated with
a mesh or discretization of the domain
. A defining feature
of these approximate trial solutions is that they are associated with
a mesh or discretization of the domain  . These
functions also have the feature that they are finite dimensional with
each dimension being associated with a node on the mesh.
. These
functions also have the feature that they are finite dimensional with
each dimension being associated with a node on the mesh.
Assume that we are given 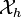 . Let us choose a weighting function
. Let us choose a weighting function
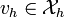 that satisfies
that satisfies 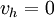 on
on 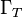 . We can
choose another function
. We can
choose another function 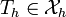 as our trial solution. Since
the boundary condition on
as our trial solution. Since
the boundary condition on 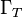 is
is 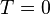 , both
, both 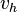 and
and 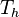 can have the same form. In the next section, we will look at the
general form of the heat equation where
can have the same form. In the next section, we will look at the
general form of the heat equation where 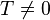 on the boundary.
on the boundary.
In finite element methods we choose trial solutions 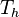 of the form
of the form
where 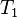 ,
, 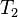 ,
, 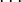 ,
, 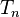 are nodal temperatures which are
constant on
are nodal temperatures which are
constant on 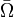 . The functions
. The functions 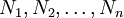 form a
basis that spans the subspace
form a
basis that spans the subspace 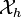 and are known as
basis functions or shape functions.
Note that
and are known as
basis functions or shape functions.
Note that  is the total number of nodes minus the number of nodes
on
is the total number of nodes minus the number of nodes
on 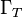 where
where 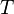 is specified.
is specified.
Since the functions 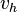 come from the same space of functions, we can
represent them as
come from the same space of functions, we can
represent them as
where 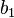 ,
, 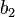 ,
, 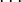 ,
, 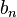 are arbitrary constant on
are arbitrary constant on 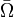 with the restriction that
with the restriction that 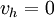 on
on 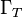 .
.
If we plug in these finite dimensional forms of 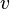 and
and 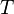 into the
variational BVP, we get an approximate form of the variational BVP
which can be stated as:
into the
variational BVP, we get an approximate form of the variational BVP
which can be stated as:
After substituting the expressions for 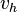 and
and 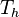 in the variational BVP
we get
in the variational BVP
we get
where,
In matrix form, we have
where ![\mathbf{b}^T = [b_1, b_2, \dots, b_n]](../I/m/053cfce70a1e9b84bf96339cd23b328e.png) ,
, 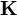 is a
is a 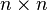 symmetric matrix,
symmetric matrix, ![\mathbf{T} = [T_1, T_2, \dots, T_n]](../I/m/7b060d312c8becac47e9a413f760412b.png) is a
is a 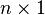 vector, and
vector, and 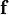 is a
is a 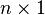 vector.
vector.
Since 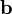 can be arbitrary, equation (38) can be further
simplified to the form
can be arbitrary, equation (38) can be further
simplified to the form
This system of equations has a solution since 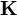 is positive-definite
and therefore has an inverse. Once the
is positive-definite
and therefore has an inverse. Once the 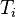 s are known, the approximate
solution can be found using
s are known, the approximate
solution can be found using
The functions 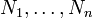 have special forms in the finite
element method that have the property that the quality of the approximation
improves with an increase in the dimension
have special forms in the finite
element method that have the property that the quality of the approximation
improves with an increase in the dimension  of the basis.
of the basis.

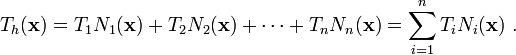
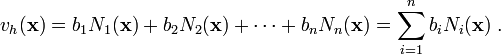

![\begin{align}
0 & = \int_{\Omega} \boldsymbol{\nabla} T_h\bullet\boldsymbol{\nabla} v_h~dV -
\int_{\Omega} f~v_h~dV \\
& = \int_{\Omega} \boldsymbol{\nabla} (T_1 N_1+\dots+T_n N_n)\bullet
\boldsymbol{\nabla} (b_1 N_1+\dots+b_n N_n)~dV -
\int_{\Omega} f~(b_1 N_1+\dots+b_n N_n)~dV \\
& = \int_{\Omega} (T_1\boldsymbol{\nabla} N_1+\dots+T_n\boldsymbol{\nabla} N_n)\bullet
(b_1\boldsymbol{\nabla} N_1+\dots+b_n\boldsymbol{\nabla} N_n)~dV
- \int_{\Omega} f~(b_1 N_1+\dots+b_n N_n)~dV \\
& = \sum_{i,j=1}^n K_{ij} T_i b_j - \sum_{j=1}^n f_j b_j \\
& = \sum_{j=1}^n b_j \left[\sum_{i=1}^n K_{ij} T_i - f_j\right] \\
\end{align}](../I/m/9d6259bbd08bde1917466d63554e773f.png)
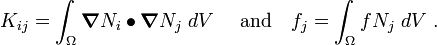
![\text{(38)} \qquad
\mathbf{b}^{T} \left[\mathbf{K} \mathbf{T} - \mathbf{f}\right] = \mathbf{0}](../I/m/255fd76491de117f2ed2caedfda06f26.png)