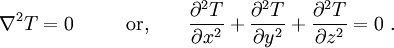Nonlinear finite elements/Quiz 1

Quiz

Answer the following questions. You have 15 minutes.

Heat conduction in an isotropic material with a constant thermal conductivity and no internal heat sources is described by Laplace's equation

\nabla^2 T = 0 ~\qquad~ \text{or,} \qquad \frac{\partial^2 T}{\partial x^2} + \frac{\partial^2 T}{\partial y^2} + \frac{\partial^2 T}{\partial z^2} = 0 ~.

Derive a symmetric weak form for the Laplace equation in 1-D (an insulated rod).
What are the expressions for the components of the finite element stiffness matrix ( 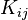$K_{ij}$ ) and the load vector ( 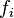$f_i$ ) for this 1-D problem?
Assume that the one of ends of the rod is maintained at a temperature of 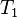$T_1$ (which is nonzero) and the other end has a prescribed heat flux of 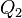$Q_2$ . If we discretize the rod into two elements, what does the reduced finite element system of equations look like? You do not have to work out the terms of the stiffness matrix - just use generic labels.
Now, assume that the thermal conductivity of the material varies with temperature. What form does the governing equation take? (We will call this the modified problem.)
List the steps needed to solve the modified problem using finite elements.

This article is issued from Wikiversity - version of the Sunday, February 22, 2009. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.