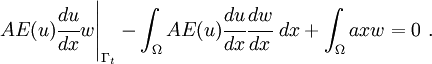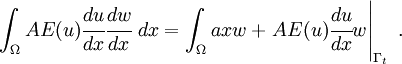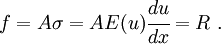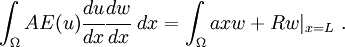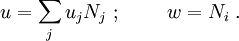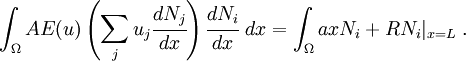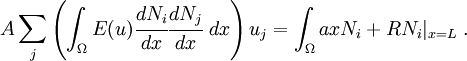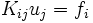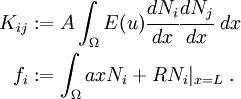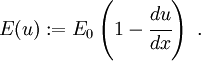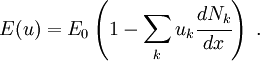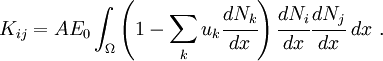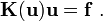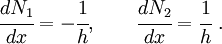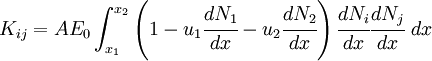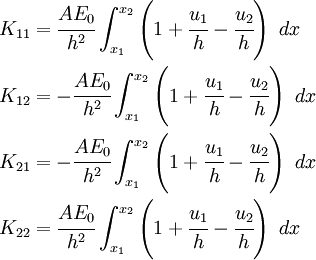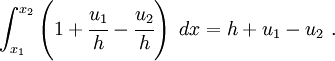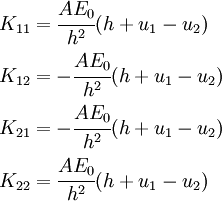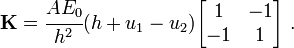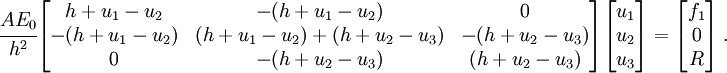Nonlinear finite elements/Nonlinear axial bar weak form
< Nonlinear finite elementsSymmetric weak form for the axially loaded bar
Let us start with the weak form and derive a symmetric stiffness matrix. We have,
Once again, we multiply with a weighting function and integrate over an element to get
Integrating the first term by parts, we get
Taking the internal force terms to the left and the external force terms to the right, we get
Note that, at  ,
,
Also, at  , we have
, we have 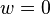 . The external surface force is zero at all other points. Therefore,
. The external surface force is zero at all other points. Therefore,
The finite element approximation
Let, the trial and weighting functions be
Then, we get
Take the constants outside the integral sign as usual, and we can write
The above can be written in the usual form as
where
This stiffness matrix is symmetric. However, we are still left with the problem of dealing with the 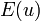 part.
part.
Dealing with 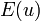
The expression of 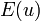 is
is
In terms of the trial function, we have
I have chosen to call the index 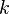 in order to distinguish it from the index names that we have already used, that is
in order to distinguish it from the index names that we have already used, that is 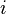 and
and 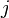 .
.
Plugging the expansion for 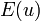 into the expression for
into the expression for 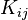 we get
we get
Notice that the stiffness matrix continues to remain symmetric when we do this because the sum over 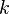 includes all the relevant nodes.
includes all the relevant nodes.
The stiffness matrix is now a function of the unknown displacements 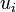 and the system of equations can be written as
and the system of equations can be written as
This is a nonlinear system of equations and cannot be solved directly (as was done for linear systems).
Making things a bit more concrete
Let us get a bit more explicit about what all that leads to.
Assume that the bar is divided into two linear elements. Therefore, there are three global nodes: 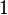 ,
, 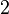 , and
, and 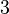 . Each element has two nodes which have local numbers
. Each element has two nodes which have local numbers 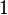 and
and 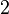 .
.
The shape functions within each element are
where  is the coordinate of node
is the coordinate of node 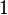 of the element, and
of the element, and 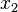 is the coordinate of node
is the coordinate of node 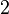 of the element. The length of the element is
of the element. The length of the element is 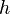 .
.
The derivatives of the shape functions are
The element stiffness matrix terms can be written as
where 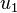 is the displacement of local node
is the displacement of local node 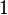 , and
, and 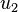 is the displacement of local node
is the displacement of local node 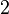 .
.
Plugging in the values of the derivatives of the shape functions, we get
The terms inside the integrals are the same for all the coefficients of the stiffness matrix (this is not true in general), and we have
Therefore,
In matrix form, the element stiffness matrix is
For simplicity, let us set the body force term 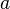 to zero. Let us also assume that both elements have equal lengths. Then the assembled global system of equations (for the two element mesh) is
to zero. Let us also assume that both elements have equal lengths. Then the assembled global system of equations (for the two element mesh) is
After simplification, we have
The stiffness matrix is a function of 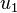 ,
, 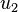 , and
, and 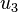 .
.
The boundary condition at 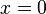 is
is 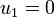 . Therefore, the reduced system of equations can be written as
. Therefore, the reduced system of equations can be written as
The reduced stiffness matrix is a function of 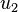 and
and 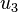 .
.
How can we find 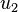 and
and 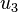 under these circumstances? We will use the Newton-Raphson numerical technique.
under these circumstances? We will use the Newton-Raphson numerical technique.
![{
A~\cfrac{d}{dx}\left[E(u)\cfrac{du}{dx}\right] + ax = 0 ~.
}](../I/m/dbb1480fc327297e9111f9eb984f2aad.png)
![\int_{\Omega} A~\cfrac{d}{dx}\left[E(u)\cfrac{du}{dx}\right]w~dx +
\int_{\Omega} axw = 0 ~.](../I/m/43ae9333d91dc6b4dbf1ad44ad57540a.png)