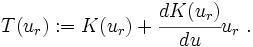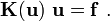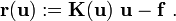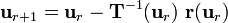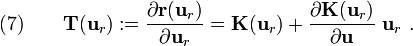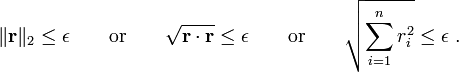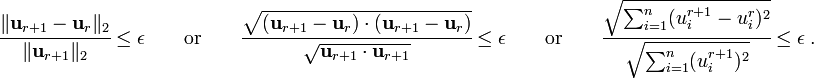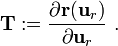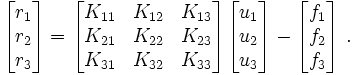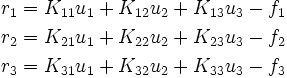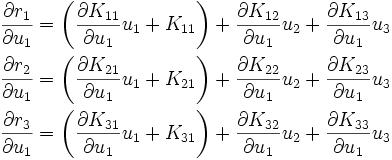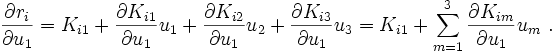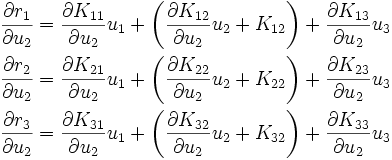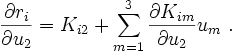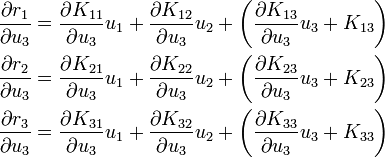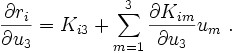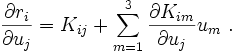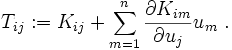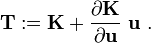Nonlinear finite elements/Newton method for finite elements
< Nonlinear finite elementsNewton's method for nonlinear finite elements
The finite element system of equations is of the form
In order to write it in the form 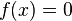 , we define the residual
, we define the residual
Then, the Newton iteration formula becomes
The slope of the tangent (the tangent stiffness) is
Therefore the tangent stiffness is
So far we have considered Newton's method only for single equations. What changes have to be made for a system of equations such as the ones encountered in FEM?
Newton's method for a system of equations
For a system of equations, all we have to do is a straightforward extension of the method as it applies to one dimension. In this case, it's easier to think in terms of matrices instead of individual coefficients of the matrices. Thus, we have
The residual is defined as
Then, the Newton iteration formula is
where the tangent stiffness matrix is given by
The iterative procedure is terminated when either the residual is very small or the difference between successive solutions is less than a specified tolerance.
However, both the residual 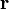 and the solution
and the solution 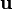 are vectors. We usually compare the
are vectors. We usually compare the 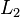 (Euclidean) norm of the vectors with a tolerance
(Euclidean) norm of the vectors with a tolerance  . In symbolic form, we check the norm of the residual using
. In symbolic form, we check the norm of the residual using
For the difference between successive solutions we check
How do we calculate the derivative of 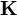 with respect to
with respect to 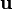 ?
?
In equation (7) we have a terms that involves a partial derivative of matrix 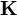 with respect to the vector
with respect to the vector 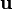 . To see what that means, let us look at the component form of the tangent stiffness matrix.
. To see what that means, let us look at the component form of the tangent stiffness matrix.
The tangent stiffness matrix is defined as
Let us consider a 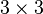 stiffness matrix and see what the above equation means. The residual is
stiffness matrix and see what the above equation means. The residual is
Expanding the above matrix equation out we get
Taking derivatives with respect to 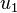 , we get
, we get
In shorter form, we can write
Similarly, taking derivatives with respect to 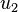 , we get
, we get
The short form of the above is
Finally, taking derivatives with respect to 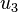 gives us
gives us
The short form is
Combining the three short forms of the 9 equations, we get
Each of these terms represents one component 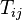 of the matrix
of the matrix 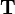 ,
and for a
,
and for a 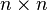 stiffness matrix we get
stiffness matrix we get
In matrix notation, the above equation is written as
This shows us how to compute the derivative of 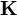 with respect to
with respect to 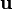 and hence
and hence 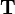 .
.
Note that we can form the tangent stiffness matrix over an element and assemble the contributions from each element to get the global tangent stiffness matrix. The reasons are the same as those for the standard global stiffness matrix.
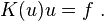

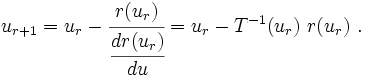
![\begin{align}
T(u_r) := \cfrac{dr(u_r)}{du}
& = \cfrac{d}{du}[K(u) u - f]\ \\
& = K(u) + \cfrac{dK(u)}{du}u\ \\
& = K(u_r) + \cfrac{dK(u_r)}{du}u_r
\end{align}](../I/m/9b0271c484706ddef1492d5b33b01907.png)