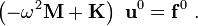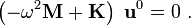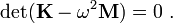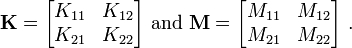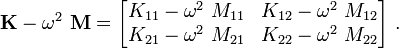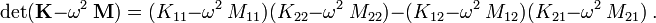Nonlinear finite elements/Natural vibration
< Nonlinear finite elementsSpecial Case: Natural Vibrations
Recall that the finite element system of equations has the form
We could also have written this equation as
For natural vibrations, the forces and the displacements are assumed to be periodic in time, i.e.,
and
Then, the accelerations take the form
Plugging these into the FE system of equations, we get
After simplification, we get
If there is no forcing, the right hand side is zero, and we get the finite element system of equations for free vibrations
The above equation is similar to the eigenvalue problem of the form
Since the right hand side is zero, the finite element system of equations has a solution only if
For a two noded element,
Therefore,
The determinant is
This gives us a quadratic equation in 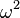 which can be solved
to find the natural frequencies of the element.
which can be solved
to find the natural frequencies of the element.
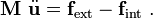
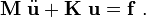
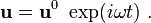
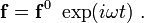
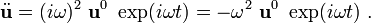
![[-\omega^2~\exp(i\omega t)]\mathbf{M}~\mathbf{u}^0 + \exp(i\omega t)~\mathbf{K}~\mathbf{u}^0 =
\exp(i\omega t)~\mathbf{f}^0 ~.](../I/m/e68ca97f0778444b3dd76424a2860017.png)