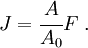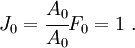Nonlinear finite elements/Motion in Lagrangian form
< Nonlinear finite elementsMotion in Lagrangian Form
The motion is given by
For the reference configuration,
The displacement is
For the reference configuration,
The deformation gradient is
For the reference configuration,
The Jacobian determinant of the motion is
For the reference configuration,
This article is issued from Wikiversity - version of the Wednesday, August 15, 2007. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.
![{
x = \varphi(X, t) = x(X, t) ~, ~~\qquad X \in [0, L_0]~.
}](../I/m/4095c80ff774f3420de13976b7b2869f.png)
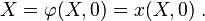
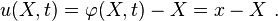
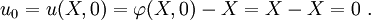
![{
F(X, t) = \frac{\partial }{\partial X}[\varphi(X,t)] = \frac{\partial x}{\partial X} ~.
}](../I/m/5f80c063add10f87bb7f48fa8024001c.png)
![F_0 = F(X, 0) = \frac{\partial }{\partial X}[\varphi(X,0)] = \frac{\partial X}{\partial X} = 1 ~.](../I/m/980a28c610735bdfb8d21b99c93dd115.png)