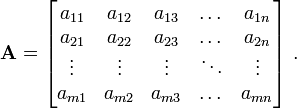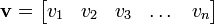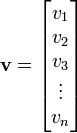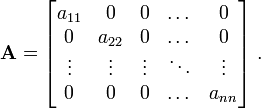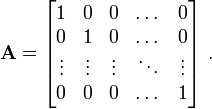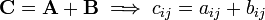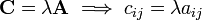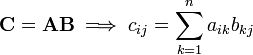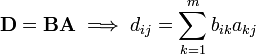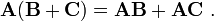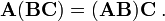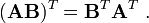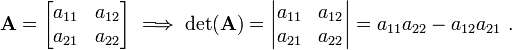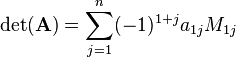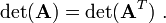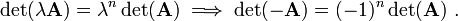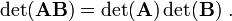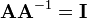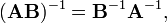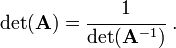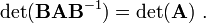Nonlinear finite elements/Matrices
< Nonlinear finite elementsMuch of finite elements revolves around forming matrices and solving systems of linear equations using matrices. This learning resource gives you a brief review of matrices.
Matrices
Suppose that you have a linear system of equations
Matrices provide a simple way of expressing these equations. Thus, we can instead write
An even more compact notation is
Here  is a
is a 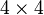 matrix while
matrix while  and
and 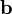 are
are 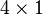 matrices. In general, an
matrices. In general, an 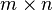 matrix
matrix  is a set of numbers
arranged in
is a set of numbers
arranged in 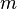 rows and
rows and  columns.
columns.
Practice Exercises
Practice: Expressing Linear Equations As Matrices
Types of Matrices
Common types of matrices that we encounter in finite elements are:
- a row vector that has one row and
 columns.
columns.
- a column vector that has
 rows and one column.
rows and one column.
- a square matrix that has an equal number of rows and columns.
- a diagonal matrix which is a square matrix with only the
diagonal elements (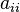 ) nonzero.
) nonzero.
- the identity matrix (
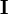 ) which is a diagonal matrix and
) which is a diagonal matrix and
with each of its nonzero elements (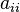 ) equal to 1.
) equal to 1.
- a symmetric matrix which is a square matrix with elements
such that  .
.
- a skew-symmetric matrix which is a square matrix with elements
such that 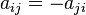 .
.
Note that the diagonal elements of a skew-symmetric matrix have to be zero: 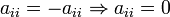 .
.
Matrix addition
Let  and
and 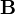 be two
be two 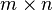 matrices with components
matrices with components 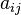 and
and 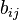 , respectively. Then
, respectively. Then
Multiplication by a scalar
Let  be a
be a 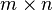 matrix with components
matrix with components 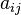 and let
and let
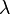 be a scalar quantity. Then,
be a scalar quantity. Then,
Multiplication of matrices
Let  be a
be a 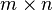 matrix with components
matrix with components 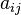 . Let
. Let 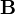 be a
be a 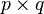 matrix with components
matrix with components 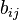 .
.
The product 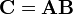 is defined only if
is defined only if 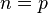 . The matrix
. The matrix 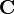 is a
is a 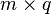 matrix with components
matrix with components  . Thus,
. Thus,
Similarly, the product 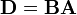 is defined only if
is defined only if 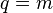 . The matrix
. The matrix 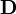 is a
is a 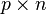 matrix with components
matrix with components 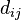 . We have
. We have
Clearly, 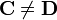 in general, i.e., the matrix product is not
commutative.
in general, i.e., the matrix product is not
commutative.
However, matrix multiplication is distributive. That means
The product is also associative. That means
Transpose of a matrix
Let  be a
be a 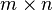 matrix with components
matrix with components 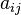 . Then the transpose of the matrix is defined as the
. Then the transpose of the matrix is defined as the 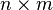 matrix
matrix 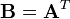 with components
with components 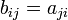 . That is,
. That is,
An important identity involving the transpose of matrices is
Determinant of a matrix
The determinant of a matrix is defined only for square matrices.
For a 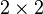 matrix
matrix  , we have
, we have
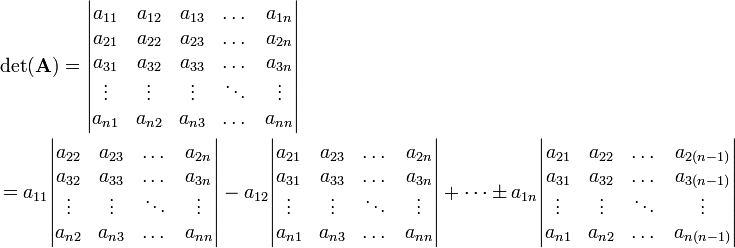
For a 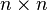 matrix, the determinant is calculated by expanding into
minors as
matrix, the determinant is calculated by expanding into
minors as
In short, the determinant of a matrix  has the value
has the value
where 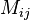 is the determinant of the submatrix of
is the determinant of the submatrix of  formed
by eliminating row
formed
by eliminating row 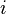 and column
and column 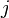 from
from  .
.
Some useful identities involving the determinant are given below.
- If
 is a
is a 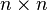 matrix, then
matrix, then
- If
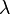 is a constant and
is a constant and  is a
is a 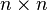 matrix, then
matrix, then
- If
 and
and 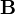 are two
are two 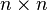 matrices, then
matrices, then
If you think you understand determinants, take the quiz.
Inverse of a matrix
Let  be a
be a 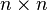 matrix. The inverse of
matrix. The inverse of  is denoted by
is denoted by 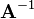 and is defined such that
and is defined such that
where 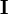 is the
is the 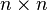 identity matrix.
identity matrix.
The inverse exists only if 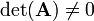 . A singular matrix
does not have an inverse.
. A singular matrix
does not have an inverse.
An important identity involving the inverse is
since this leads to:
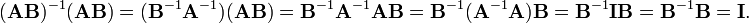
Some other identities involving the inverse of a matrix are given below.
- The determinant of a matrix is equal to the multiplicative inverse of the
determinant of its inverse.
- The determinant of a similarity transformation of a matrix
is equal to the original matrix.
We usually use numerical methods such as Gaussian elimination to compute the inverse of a matrix.
Eigenvalues and eigenvectors
A thorough explanation of this material can be found at Eigenvalue, eigenvector and eigenspace. However, for further study, let us consider the following examples:
- Let :
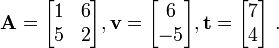
Which vector is an eigenvector for  ?
?
We have
 , and
, and 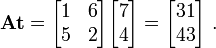
Thus, 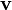 is an eigenvector.
is an eigenvector.
- Is
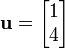 an eigenvector for
an eigenvector for 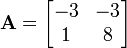 ?
?
We have that since 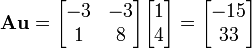 ,
, 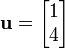 is not an eigenvector for
is not an eigenvector for 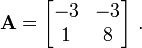
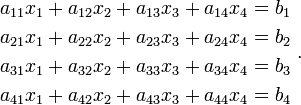

![\left[\mathsf{A}\right] \left[\mathsf{x}\right] = \left[\mathsf{b}\right] ~~~~\text{or}~~~~ \mathbf{A} \mathbf{x} = \mathbf{b} ~.](../I/m/9ab65143e05a0e68423b953fbc300fc3.png)