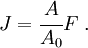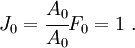Nonlinear finite elements/Lagrangian finite elements
< Nonlinear finite elementsLagrangian Finite Elements
Two types of approaches are usually taken when formulating Lagrangian finite elements:
- Total Lagrangian:
- The stress and strain measures are Lagrangian, i.e.,they are defined with respect to the original configuration.
- Derivatives and integrals are computed with respect to the Lagrangian (or material) coordinates
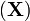 .
.
- Updated Lagrangian:
- The stress and strain measures are Eulerian, i.e.,they are defined with respect to the current configuration.
- Derivatives and integrals are computed with respect to the Eulerian (or spatial) coordinates
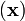 .
.
The following 1-D examples illustrate what these approaches entail.
Consider the axially loaded bar shown in Figure 1.
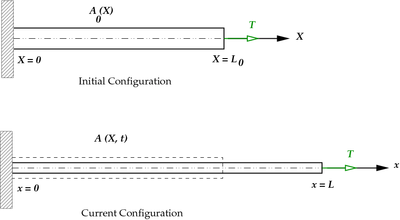 Figure 1. Axially loaded bar |
In the reference (or initial) configuration, the bar has a length 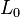 ,
an area
,
an area 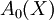 , and density
, and density 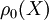 . A tensile force
. A tensile force 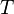 is applied at the free end. In the current (or deformed) configuration at time
is applied at the free end. In the current (or deformed) configuration at time 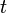 , the length of the bar increases to
, the length of the bar increases to 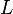 , the area decreases to
, the area decreases to 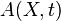 , and the density changes to
, and the density changes to 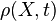 .
.
Motion in Lagrangian Form
The motion is given by
For the reference configuration,
The displacement is
For the reference configuration,
The deformation gradient is
For the reference configuration,
The Jacobian determinant of the motion is
For the reference configuration,
This article is issued from Wikiversity - version of the Wednesday, August 15, 2007. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.
![{
x = \varphi(X, t) = x(X, t) ~, ~~\qquad X \in [0, L_0]~.
}](../I/m/4095c80ff774f3420de13976b7b2869f.png)
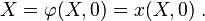
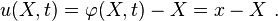
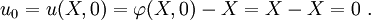
![{
F(X, t) = \frac{\partial }{\partial X}[\varphi(X,t)] = \frac{\partial x}{\partial X} ~.
}](../I/m/5f80c063add10f87bb7f48fa8024001c.png)
![F_0 = F(X, 0) = \frac{\partial }{\partial X}[\varphi(X,0)] = \frac{\partial X}{\partial X} = 1 ~.](../I/m/980a28c610735bdfb8d21b99c93dd115.png)