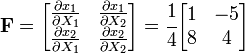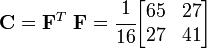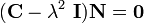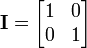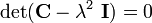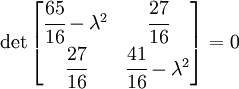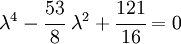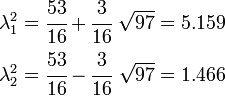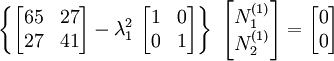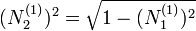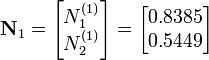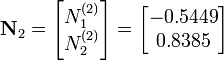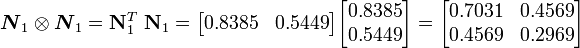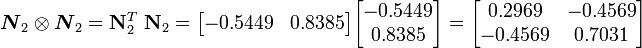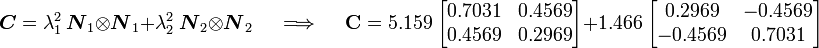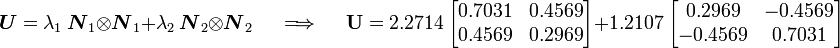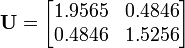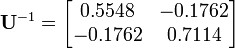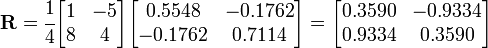Nonlinear finite elements/Kinematics - polar decomposition
< Nonlinear finite elementsPolar decomposition
The w:Polar decomposition theorem states that any second order tensor whose determinant is positive can be decomposed uniquely into a symmetric part and an orthogonal part.
In continuum mechanics, the deformation gradient 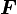 is such a tensor
because
is such a tensor
because 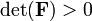 . Therefore we can write
. Therefore we can write
where 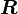 is an orthogonal tensor (
is an orthogonal tensor (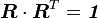 ) and
) and 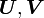 are symmetric tensors (
are symmetric tensors (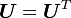 and
and 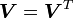 ) called the
right stretch tensor and the left stretch tensor, respectively.
This decomposition is called the polar decomposition of
) called the
right stretch tensor and the left stretch tensor, respectively.
This decomposition is called the polar decomposition of 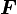 .
.
Recall that the right Cauchy-Green deformation tensor is defined as
Clearly this is a symmetric tensor. From the polar decomposition of 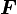 we have
we have
If you know 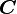 then you can calculate
then you can calculate 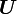 and hence
and hence 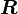 using
using
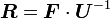 .
.
How do you find the square root of a tensor?
If you want to find 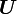 given
given 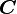 you will need to take the square root of
you will need to take the square root of 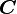 . How does one do that?
. How does one do that?
We use what is called the spectral decomposition or eigenprojection of 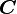 . The spectral decomposition involves expressing
. The spectral decomposition involves expressing 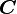 in terms of its eigenvalues and eigenvectors. The tensor product of the eigenvectors acts as a basis while the eigenvalues give the magnitude of the projection.
in terms of its eigenvalues and eigenvectors. The tensor product of the eigenvectors acts as a basis while the eigenvalues give the magnitude of the projection.
Thus,
where 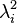 are the principal values (eigenvalues) of
are the principal values (eigenvalues) of 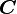 and
and 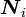 are the principal directions (eigenvectors) of
are the principal directions (eigenvectors) of 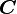 .
.
Therefore,
Since the basis does not change, we then have
Therefore the 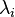 can be interpreted as principal stretches and
the vectors
can be interpreted as principal stretches and
the vectors 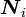 are the directions of the principal stretches.
are the directions of the principal stretches.
Exercise:
If
show that
Example of polar decomposition
Let us assume that the motion is given by
The adjacent figure shows how a unit square subjected to this motion evolves over time.
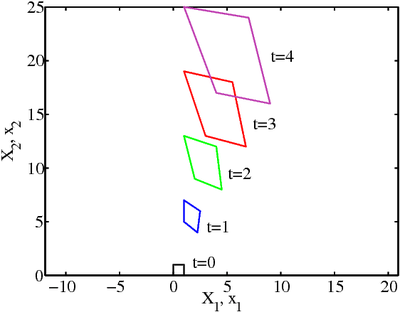 An example of a motion. |
Deformation gradient
The deformation gradient is given by
Therefore
At 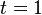 at the position
at the position 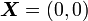 we have
we have
You can calculate the deformation gradient at other points in a similar manner.
Right Cauchy-Green deformation tensor
We have
Therefore,
To compute 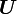 we have to find the eigenvalues and eigenvectors of
we have to find the eigenvalues and eigenvectors of 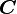 .
The eigenvalue problem is
.
The eigenvalue problem is
where
To find the eigenvalues we solve the characteristic equation
Plugging in the numbers, we get
or
This equation has two solutions
Taking the square roots we get the values of the principal stretches
To compute the eigenvectors we plug into the eigenvalues into the eigenvalue problem to get
Because this system of equations is not linearly independent, we need another equation to solve this system of equations for 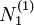 and
and 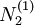 .
This problem is eliminated by using the following equation (which implies that
.
This problem is eliminated by using the following equation (which implies that 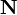 is a unit vector)
is a unit vector)
Solving, we get
We can do the same thing for the other eigenvector 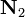 to get
to get
Therefore,
and
Therefore,
We usually don't see any problem to calculate 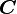 at this point and go straight to the right stretch tensor.
at this point and go straight to the right stretch tensor.
Right stretch
The right stretch tensor 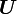 is given by
is given by
or
We can invert this matrix to get
Rotation
We can now find the rotation matrix by using th relation
In matrix form,
You can check whether this matrix is orthogonal by seeing whether
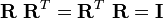 .
.
You thus get the polar decomposition of 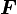 . In an actual calculation you have to be careful about floating point errors. Otherwise you might not get a matrix that is orthogonal.
. In an actual calculation you have to be careful about floating point errors. Otherwise you might not get a matrix that is orthogonal.
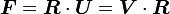
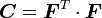
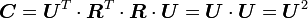
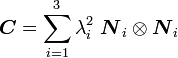
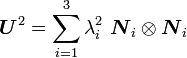
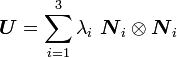
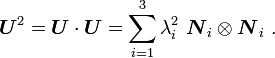
![\begin{align}
x_1 &= \cfrac{1}{4} \left[4~X_1 + (9 - 3~X_1 - 5~X_2 - X_1~X_2)~t\right] \\
x_2 &= X_2 + (4 + 2~X_1)~t
\end{align}](../I/m/a8500c1db5164baa385635977fb116a2.png)
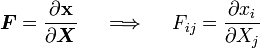
![\begin{align}
F_{11} &= \frac{\partial x_1}{\partial X_1} = \cfrac{1}{4}\left[4 + (- 3 - X_2)~t\right] \\
F_{12} &= \frac{\partial x_1}{\partial X_2} = \cfrac{1}{4}\left[(- 5 - X_1)~t\right] \\
F_{21} &= \frac{\partial x_2}{\partial X_1} = 2~t \\
F_{22} &= \frac{\partial x_2}{\partial X_2} = 1
\end{align}](../I/m/c39a96d1d5a09b49f15e3058348641e0.png)