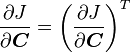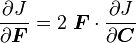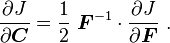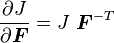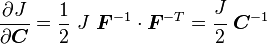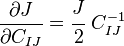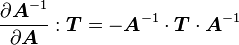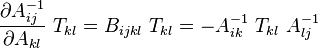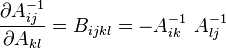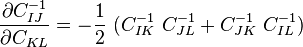Nonlinear finite elements/Kinematics
< Nonlinear finite elementsStrain Measures in three dimensions
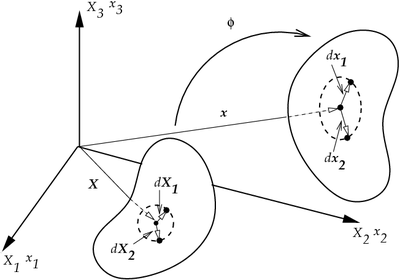 The motion of a body |
Initial orthonormal basis:
Deformed orthonormal basis:
We assume that these coincide.
Motion
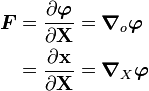
Deformation Gradient
Effect of 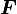 :
:
Dyadic notation:
Index notation:
The determinant of the deformation gradient is usually denoted by 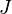 and is a measure of the change in volume, i.e.,
and is a measure of the change in volume, i.e.,
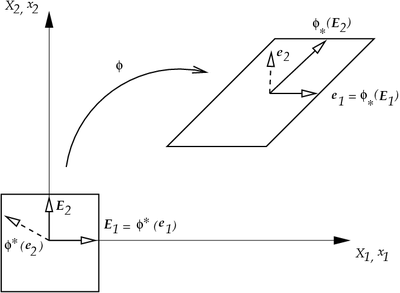
Push Forward and Pull Back
Forward Map:
Forward deformation gradient:
Dyadic notation:
Effect of deformation gradient:
Push Forward operation:
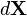 = material vector.
= material vector.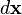 = spatial vector.
= spatial vector.
Inverse map:
Inverse deformation gradient:
Dyadic notation:
Effect of inverse deformation gradient:
Pull Back operation:
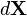 = material vector.
= material vector.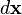 = spatial vector.
= spatial vector.
Example
 Push forward and pull back |
Motion:
Deformation Gradient:
Inverse Deformation Gradient:
Push Forward:
Pull Back:
Cauchy-Green Deformation Tensors
Right Cauchy-Green Deformation Tensor
Recall:
Therefore,
Using index notation:
Right Cauchy-Green tensor:
Left Cauchy-Green Deformation Tensor
Recall:
Therefore,
Using index notation:
Left Cauchy-Green (Finger) tensor:
Strain Measures
Green (Lagrangian) Strain
Green strain tensor:
Index notation:
Almansi (Eulerian) Strain
Almansi strain tensor:
Index notation:
Push Forward and Pull Back
Recall:
Now,
Therefore,
Push Forward:
Pull Back:
Some useful results
Derivative of J with respect to the deformation gradient
We often need to compute the derivative of 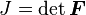 with respect the the deformation gradient
with respect the the deformation gradient 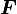 . From tensor calculus we have, for any second order tensor
. From tensor calculus we have, for any second order tensor 
Therefore,
|
|
Derivative of J with respect to the right Cauchy-Green deformation tensor
The derivative of J with respect to the right Cauchy-Green deformation tensor (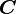 ) is also often encountered in continuum mechanics.
) is also often encountered in continuum mechanics.
To calculate the derivative of 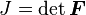 with respect to
with respect to 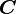 , we recall that (for any second order tensor
, we recall that (for any second order tensor 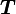 )
)
Also,
From the symmetry of 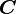 we have
we have
Therefore, involving the arbitrariness of 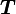 , we have
, we have
Hence,
Also recall that
Therefore,
|
|
In index notation,
|
|
Derivative of the inverse of the right Cauchy-Green tensor
Another result that is often useful is that for the derivative of the inverse of the right Cauchy-Green tensor (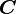 ).
).
Recall that, for a second order tensor  ,
,
In index notation
or,
Using this formula and noting that since 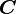 is a symmetric second order tensor, the derivative of its inverse is a symmetric fourth order tensor we have
is a symmetric second order tensor, the derivative of its inverse is a symmetric fourth order tensor we have
|
|
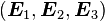
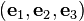
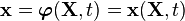
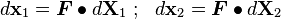
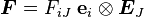
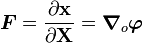
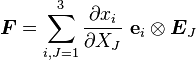
![d\mathbf{x} = \boldsymbol{F}\bullet d\mathbf{X} = \boldsymbol{\varphi}_{*}[d\mathbf{X}]](../I/m/8cc2874844bb7e1d3b51dd7d3cd98598.png)
![\boldsymbol{\varphi}_{*}[\bullet]](../I/m/a62dde81b2f0ea0d36cef87e859ef097.png)
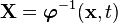
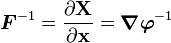
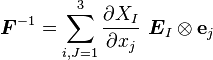
![d\mathbf{X} = \boldsymbol{F}^{-1}\bullet d\mathbf{x} = \boldsymbol{\varphi}^{*}[d\mathbf{x}]](../I/m/92ef183279d680633722725c3cf1b3e7.png)
![\boldsymbol{\varphi}^{*}[\bullet]](../I/m/810155202807314bfd2857beef4128e2.png)
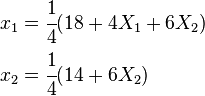
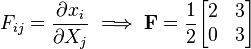
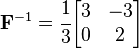
![\begin{align}
\boldsymbol{\varphi}_{*}[\boldsymbol{E}_1] & = \mathbf{F}\begin{bmatrix} 1 \\ 0 \end{bmatrix}
= \begin{bmatrix} 1 \\ 0 \end{bmatrix} \\
\boldsymbol{\varphi}_{*}[\boldsymbol{E}_2] & = \mathbf{F}\begin{bmatrix} 0 \\ 1 \end{bmatrix}
= \begin{bmatrix} 1.5 \\ 1.5 \end{bmatrix}
\end{align}](../I/m/7df5aec89188587702ad30897a3e7cd5.png)
![\begin{align}
\boldsymbol{\varphi}^{*}[\mathbf{e}_1] & = \mathbf{F}^{-1}\begin{bmatrix} 1 \\ 0 \end{bmatrix}
= \begin{bmatrix} 1 \\ 0 \end{bmatrix} \\
\boldsymbol{\varphi}^{*}[\mathbf{e}_2] & = \mathbf{F}^{-1}\begin{bmatrix} 0 \\ 1 \end{bmatrix}
= \begin{bmatrix} -1 \\ 2/3 \end{bmatrix}
\end{align}](../I/m/9924fa7fd1e5f47b92172298215227a0.png)
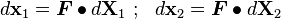
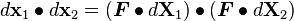
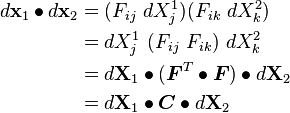
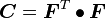
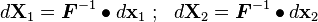
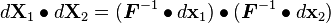
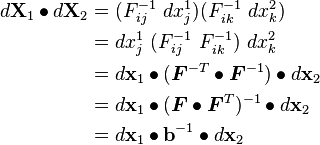
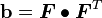
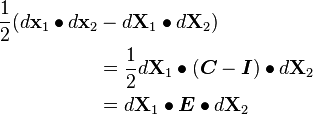
![\begin{align}
\boldsymbol{E} & = \frac{1}{2}(\boldsymbol{C} - \boldsymbol{I}) \\
& = \frac{1}{2}(\boldsymbol{F}^T\bullet\boldsymbol{F} - \boldsymbol{I}) \\
& = \frac{1}{2}\left[\boldsymbol{\nabla}_o \mathbf{u} + (\boldsymbol{\nabla}_o \mathbf{u})^T
+ \boldsymbol{\nabla}_o \mathbf{u}\bullet(\boldsymbol{\nabla_o \mathbf{u})^T}\right]
\end{align}](../I/m/7698d1512520db7e8e8590ccd335f016.png)
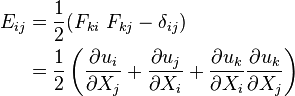
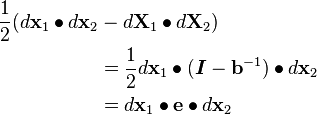
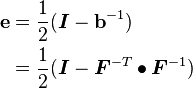
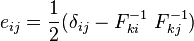
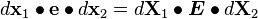
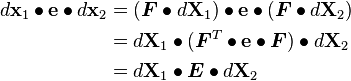
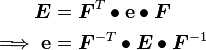
![\mathbf{e} = \boldsymbol{\varphi}_{*}[\boldsymbol{E}] =\boldsymbol{F}^{-T}\bullet\boldsymbol{E}\bullet\boldsymbol{F}^{-1}](../I/m/94a5b2b9eb1c4bdb5a47aa738ad5c40d.png)
![\boldsymbol{E} = \boldsymbol{\varphi}^{*}[\mathbf{e}] =\boldsymbol{F}^T\bullet\mathbf{e}\bullet\boldsymbol{F}](../I/m/d4cdd4696b6d960d661635597e15ffdf.png)
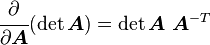
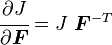
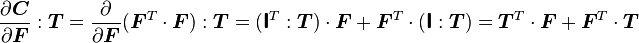
![\frac{\partial J}{\partial \boldsymbol{F}}:\boldsymbol{T} = \frac{\partial J}{\partial \boldsymbol{C}}:(\frac{\partial \boldsymbol{C}}{\partial \boldsymbol{F}}:\boldsymbol{T})
= \frac{\partial J}{\partial \boldsymbol{C}}:(\boldsymbol{T}^T\cdot\boldsymbol{F} + \boldsymbol{F}^T\cdot\boldsymbol{T})
= \left[\boldsymbol{F}\cdot\frac{\partial J}{\partial \boldsymbol{C}}\right]:\boldsymbol{T} +
\left[\boldsymbol{F}\cdot\left(\frac{\partial J}{\partial \boldsymbol{C}}\right)^T\right]:\boldsymbol{T}](../I/m/93aba78f4bf303087a44529fdbd5117c.png)