Nonlinear finite elements/Homework 5/Solutions/Problem 1
< Nonlinear finite elements < Homework 5 < SolutionsProblem 1: Nonlinear Beam Bending
Given:
The differential equations governing the bending of straight beams are
Solution
Part 1
Show that the weak forms of these equations can be written as
First we get rid of the shear force term by combining the second and third equations to get
Let 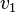 be the weighting function for equation (1) and let
be the weighting function for equation (1) and let 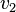 be the weighting function for equation (2).
be the weighting function for equation (2).
Then the weak forms of the two equations are
To get the symmetric weak forms, we integrate by parts (even though the symmetry is not obvious at this stage) to get
Integrate equation (6) again by parts, and get
Collect terms and rearrange equations (5) and (7) to get
Rewriting the equations, we get
Hence shown.
Part 2
The von Karman strains are related to the displacements by
The stress and moment resultants are defined as
For a linear elastic material, the stiffnesses of the beam in extension and bending are defined as
where  is the Young's modulus of the material.
is the Young's modulus of the material.
Derive expressions for 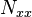 and
and 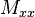 in terms of the displacements
in terms of the displacements 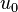 and
and 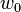 and the extensional and bending stiffnesses of the beam assuming a linear elastic material.
and the extensional and bending stiffnesses of the beam assuming a linear elastic material.
The stress-strain relations for an isotropic linear elastic material are
Since all strains other than 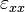 are zero, the above equations reduce to
are zero, the above equations reduce to
If we ignore the stresses 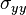 and
and 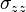 , the only allowable value of
, the only allowable value of 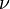 is zero. Then the stress-strain relations become
is zero. Then the stress-strain relations become
Plugging this relation into the stress and moment of stress resultant equations, we get
Plugging in the relations for the strain we get
Since both 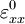 and
and 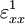 are independent of
are independent of 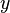 and
and 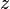 , we can take these quantities outside the integrals and get
, we can take these quantities outside the integrals and get
Using the definitions of the extensional, extensional-bending, and bending stiffness, we can then write
To write these relations in terms of 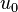 and
and 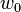 we substitute the expressions for the von Karman strains to get
we substitute the expressions for the von Karman strains to get
These are the expressions of the resultants in terms of the displacements.
Part 3
Express the weak forms in terms of the displacements and the extensional and bending stiffnesses.
The weak form equations are
At this stage we make two more assumptions:
- The elastic modulus is constant throughout the cross-section.
- The
 -axis passes through the centroid of the cross-section.
-axis passes through the centroid of the cross-section.
From the first assumption, we have
From the second assumption, we get
Then the relations for 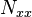 and
and 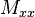 reduce to
reduce to
Let us first consider equation (11). Plugging in the expression for 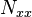 we get
we get
We can also write the above in terms of virtual displacements by defining 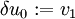 ,
, 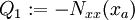 , and
, and 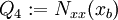 . Then we get
. Then we get
Next, we do the same for equation (12). Plugging in the expressions for 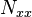 and
and 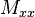 , we get
, we get
We can write the above in terms of the virtual displacements and the generalized forces by defining
to get
Part 4
Assume that the approximate solutions for the axial displacement and the transverse deflection over a two noded element are given by
where 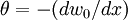 .
.
Compute the element stiffness matrix for the element.
The weak forms of the governing equations are
Let us first write the approximate solutions as
where 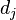 are generalized displacements and
are generalized displacements and
To formulate the finite element system of equations, we substitute the expressions from 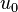 and
and 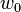 from equations (19) and (20) into the weak form, and substitute the shape functions
from equations (19) and (20) into the weak form, and substitute the shape functions 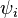 for
for 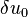 ,
, 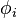 for
for 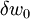 .
.
For the first equation (17) we get
After reorganizing, we have
We can write the above as
where 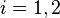 and
and
For the second equation (18) we get
After rearranging we get
We can write the above as
where 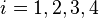 and
and
In matrix form, we can write
or
The finite element system of equations can then be written as
or
Part 5
Show the alternate procedure by which the element stiffness matrix can be made symmetric.
The stiffness matrix is unsymmetric because 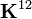 contains a factor of
contains a factor of 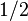 while
while 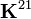 does not. The expressions of these terms are
does not. The expressions of these terms are
To get a symmetric stiffness matrix, we write equation (18) as
The quantity is green is assumed to be known from a previous iteration and adds to the 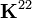 terms.
terms.
Repeating the procedure used in the previous question
After rearranging we get
We can write the above as
where 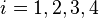 and
and
This gives us a symmetric stiffness matrix.
Part 6
Derive the element tangent stiffness matrix for the element.
Equation (21) can be written as
where
The residual is
For Newton iterations, we use the algorithm
where the tangent stiffness matrix is given by
The coefficients of the tangent stiffness matrix are given by
Recall that the finite element system of equations can be written as
where the subscripts have been changed to avoid confusion.
Therefore, the residuals are
The derivatives of the residuals with respect to the generalized displacements are
Differentiating, we get
These equations can therefore be written as
Now, the coefficients of 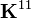 ,
, 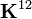 , and
, and 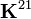 of the symmetric stiffness matrix are independent of
of the symmetric stiffness matrix are independent of 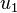 and
and 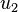 . Also, the terms of
. Also, the terms of 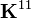 are independent of the all the generalized displacements. Therefore, the above equations reduce to
are independent of the all the generalized displacements. Therefore, the above equations reduce to
Consider the coefficients of 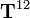 :
:
From our previous derivation, we have
Therefore,
The tangent stiffness matrix coefficients are therefore
Next, { consider the coefficients of 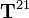 :
:
The coefficients of 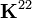 are
are
Therefore, the derivatives are
Therefore the coefficients of 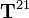 are
are
Finally, for the 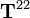 coefficients, we start with
coefficients, we start with
and plug in the derivatives of the stiffness matrix coefficients
![\begin{align}
K_{np}^{21} & = \frac{1}{2} \int_{x_a}^{x_b} \left(A_{xx} \cfrac{dw_0}{dx}\right)
\cfrac{d\phi_n}{dx}\cfrac{d\psi_p}{dx}~dx\\
K_{nq}^{22} & = \int_{x_a}^{x_b}\left\{
\frac{1}{2} A_{xx}
\left[\cfrac{du_0}{dx}+\left(\cfrac{dw_0}{dx}\right)^2\right]
\cfrac{d\phi_n}{dx}\cfrac{d\phi_q}{dx} +
D_{xx}\cfrac{d^2\phi_n}{dx^2}\cfrac{d^2\phi_q}{dx^2}\right\}~dx ~.
\end{align}](../I/m/7146e0899dfaccc2e578c247e935d730.png) \\
\\
The derivatives are
and
Therefore, the coefficients of the tangent stiffness matrix can be written as
The final expressions for the tangent stiffness matrix terms are
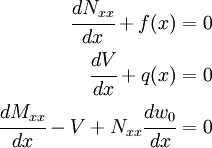
![\begin{align}
\int_{x_a}^{x_b} \cfrac{dv_1}{dx}N_{xx}~dx & =
\int_{x_a}^{x_b} v_1 f~dx + \left.v_1 N_{xx}\right|_{x_a}^{x_b}\\
\int_{x_a}^{x_b} \left[
\cfrac{dv_2}{dx}\left(\cfrac{dw_0}{dx}N_{xx}\right) -
\cfrac{d^2v_2}{dx^2}M_{xx}\right]~dx & =
\int_{x_a}^{x_b} v_2 q~dx +
\left.v_2\left(\cfrac{dw_0}{dx}N_{xx}+\cfrac{dM_{xx}}{dx}\right)
\right|_{x_a}^{x_b} -
\left.\cfrac{dv_2}{dx}M_{xx} \right|_{x_a}^{x_b}
\end{align}](../I/m/246bcd7ec2aa175a93c5bce38d888e93.png)
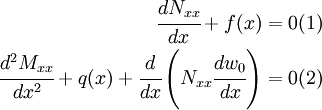
![\begin{align}
\int_{x_a}^{x_b} v_1\left(\cfrac{dN_{xx}}{dx} + f(x)\right)~dx
& = 0 \text{(3)} \qquad \\
\int_{x_a}^{x_b} v_2\left[\cfrac{d^2M_{xx}}{dx^2} + q(x) +
\cfrac{d}{dx}\left(N_{xx}\cfrac{dw_0}{dx}\right)\right]~dx & = 0
\text{(4)} \qquad
\end{align}](../I/m/736afd119a6523fc05784966ecb7cba6.png)
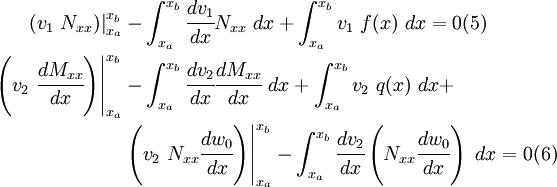
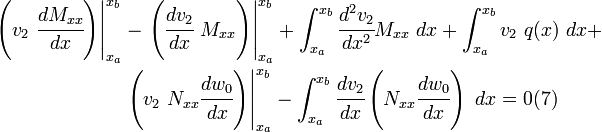
![\begin{align}
\int_{x_a}^{x_b} \cfrac{dv_1}{dx} N_{xx}~dx & =
\int_{x_a}^{x_b} v_1~f(x)~dx + \left.(v_1~N_{xx})\right|_{x_a}^{x_b}
\text{(8)} \qquad \\
\int_{x_a}^{x_b} \left[
\cfrac{dv_2}{dx}\left(N_{xx}\cfrac{dw_0}{dx}\right) -
\cfrac{d^2v_2}{dx^2}M_{xx}\right]~dx & =
\int_{x_a}^{x_b} v_2~q(x)~dx +\\
&\left[\left(v_2~\cfrac{dM_{xx}}{dx}\right) -
\left(\cfrac{dv_2}{dx}~M_{xx}\right) +
\left(v_2~N_{xx}\cfrac{dw_0}{dx}\right)\right]_{x_a}^{x_b}
\text{(9)} \qquad
\end{align}](../I/m/a392ec5272c12d2d1542dcd69b2357fc.png)
![\begin{align}
\int_{x_a}^{x_b} \cfrac{dv_1}{dx} N_{xx}~dx & =
\int_{x_a}^{x_b} v_1 f~dx + \left.v_1 N_{xx}\right|_{x_a}^{x_b} \\
\int_{x_a}^{x_b} \left[
\cfrac{dv_2}{dx}\left(N_{xx}\cfrac{dw_0}{dx}\right) -
\cfrac{d^2v_2}{dx^2}M_{xx}\right]~dx & =
\int_{x_a}^{x_b} v_2 q~dx +
\left[v_2\left(\cfrac{dM_{xx}}{dx} + N_{xx}\cfrac{dw_0}{dx}\right)
\right]_{x_a}^{x_b} -
\left[\cfrac{dv_2}{dx}~M_{xx}\right]_{x_a}^{x_b}
\end{align}
\text{(10)} \qquad](../I/m/933611fe7e48066d858c414946cea4e9.png)
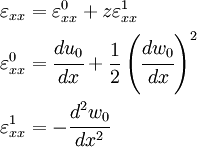
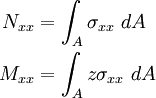

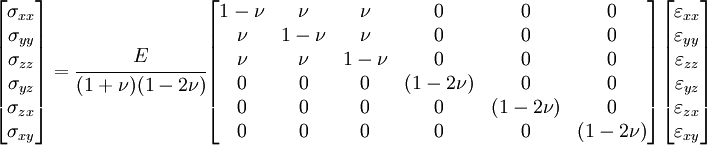
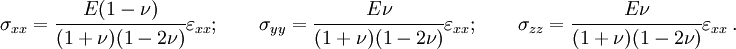
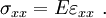
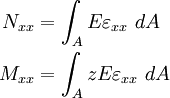
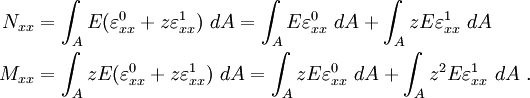
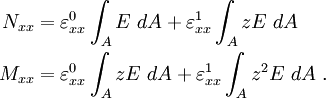
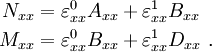
![\begin{align}
N_{xx} & =
\left[\cfrac{du_0}{dx} + \frac{1}{2}\left(\cfrac{dw_0}{dx}\right)^2\right]
A_{xx} -\cfrac{d^2w_0}{dx^2} B_{xx} \\
M_{xx} & =
\left[\cfrac{du_0}{dx} + \frac{1}{2}\left(\cfrac{dw_0}{dx}\right)^2\right]
B_{xx} -\cfrac{d^2w_0}{dx^2} D_{xx} ~.
\end{align}](../I/m/9181c0b21b42c8acbf1e4e249aa5a04d.png)
![\begin{align}
\int_{x_a}^{x_b} \cfrac{dv_1}{dx} N_{xx}~dx & =
\int_{x_a}^{x_b} v_1 f~dx + \left.v_1 N_{xx}\right|_{x_a}^{x_b}
\text{(11)} \qquad \\
\int_{x_a}^{x_b} \left[
\cfrac{dv_2}{dx}\left(N_{xx}\cfrac{dw_0}{dx}\right) -
\cfrac{d^2v_2}{dx^2}M_{xx}\right]~dx & =
\int_{x_a}^{x_b} v_2 q~dx +
\left[v_2\left(\cfrac{dM_{xx}}{dx} + N_{xx}\cfrac{dw_0}{dx}\right)
\right]_{x_a}^{x_b} -
\left[\cfrac{dv_2}{dx}~M_{xx}\right]_{x_a}^{x_b}
\text{(12)} \qquad
\end{align}](../I/m/2ae70e8d4c7407724813b3a2f8059b44.png)
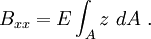
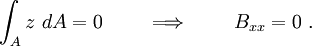
![\begin{align}
N_{xx} & =
\left[\cfrac{du_0}{dx} + \frac{1}{2}\left(\cfrac{dw_0}{dx}\right)^2\right]
A_{xx} \text{(13)} \qquad \\
M_{xx} & =- \cfrac{d^2w_0}{dx^2} D_{xx} \text{(14)} \qquad~.
\end{align}](../I/m/25ca544ee70aed1a5d8ee5219952deda.png)
![\int_{x_a}^{x_b} \cfrac{dv_1}{dx}
\left[\cfrac{du_0}{dx} + \frac{1}{2}\left(\cfrac{dw_0}{dx}\right)^2\right]
A_{xx}~dx =
\int_{x_a}^{x_b} v_1 f~dx + \left.v_1 N_{xx}\right|_{x_a}^{x_b}](../I/m/0413c77cd1574f21756828c8966e5d58.png)
![\int_{x_a}^{x_b} \cfrac{d(\delta u_0)}{dx}
\left[\cfrac{du_0}{dx} + \frac{1}{2}\left(\cfrac{dw_0}{dx}\right)^2\right]
A_{xx}~dx =
\int_{x_a}^{x_b} (\delta u_0) f~dx + \delta u_0(x_a) Q_1 +
\delta u_0(x_b) Q_4 ~.](../I/m/d54be340a6bbd353d95ee1e8c96282d3.png)
![\begin{align}
\int_{x_a}^{x_b} \left\{\cfrac{dv_2}{dx}\left(\left[\cfrac{du_0}{dx} + \cfrac{1}{2}~\left(\cfrac{dw_0}{dx}\right)^2\right] A_{xx} \cfrac{dw_0}{dx}\right)
\right. & +
\left.\cfrac{d^2 v_2}{dx^2} \left(\cfrac{d^2 w_0}{dx^2}\right) D_{xx} \right\}~dx=
\int_{x_a}^{x_b} v_2 q~dx +\\
& \left[v_2\left(\cfrac{dM_{xx}}{dx} + N_{xx}\cfrac{dw_0}{dx}\right)\right]_{x_a}^{x_b} -
\left[\cfrac{dv_2}{dx}~M_{xx}\right]_{x_a}^{x_b}
\end{align}](../I/m/0a32477c1440cc31228c68119ea8dcaa.png)
![\begin{align}
\delta w_0 & := v_2 \\
\delta \theta & := \cfrac{dv_2}{dx} \\
Q_2 & := -\left[\cfrac{dM_{xx}}{dx} + N_{xx}\cfrac{dw_0}{dx}\right]_{x_a} \\
Q_5 & := \left[\cfrac{dM_{xx}}{dx} + N_{xx}\cfrac{dw_0}{dx}\right]_{x_b} \\
Q_3 & := -M_{xx} (x_a) \\
Q_6 & := M_{xx} (x_b)
\end{align}](../I/m/2c87e33db9ec721544c6c94e05dec149.png)
![\begin{align}
\int_{x_a}^{x_b} \left\{\cfrac{d(\delta w_0)}{dx} \right. &
\left[\cfrac{du_0}{dx} + \cfrac{1}{2}~\left(\cfrac{dw_0}{dx}\right)^2\right] \cfrac{dw_0}{dx} A_{xx} +
\left.\cfrac{d^2(\delta w_0)}{dx^2} \left(\cfrac{d^2w_0}{dx^2}\right) D_{xx} \right\}~dx= \\
& \int_{x_a}^{x_b} (\delta w_0) q~dx +
\delta w_0(x_a) Q_2 + \delta w_0(x_b) Q_5 +
\delta \theta(x_a) Q_3 +
\delta \theta(x_b) Q_6 ~.
\end{align}](../I/m/802cd0e03048512917f331c488123904.png)
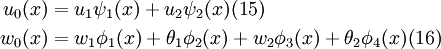
![\begin{align}
\int_{x_a}^{x_b} \cfrac{d(\delta u_0)}{dx} &
\left[\cfrac{du_0}{dx} + \frac{1}{2}\left(\cfrac{dw_0}{dx}\right)^2\right]
A_{xx}~dx =
\int_{x_a}^{x_b} (\delta u_0) f~dx + \delta u_0(x_a) Q_1 +
\delta u_0(x_b) Q_4 \text{(17)} \qquad \\
\int_{x_a}^{x_b} \left\{\cfrac{d(\delta w_0)}{dx} \right. &
\left[\cfrac{du_0}{dx} + \cfrac{1}{2}~\left(\cfrac{dw_0}{dx}\right)^2\right] \cfrac{dw_0}{dx} A_{xx} +
\left.\cfrac{d^2(\delta w_0)}{dx^2} \left(\cfrac{d^2w_0}{dx^2}\right) D_{xx} \right\}~dx =
\\
& \int_{x_a}^{x_b} (\delta w_0) q~dx +
\delta w_0(x_a) Q_2 + \delta w_0(x_b) Q_5 +
\delta \theta(x_a) Q_3 +
\delta \theta(x_b) Q_6 ~. \text{(18)} \qquad
\end{align}](../I/m/4c2ecccc268c7986c461a45a2aacc71c.png)
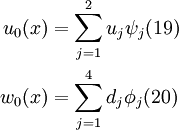
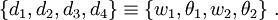
![\int_{x_a}^{x_b} \cfrac{d\psi_i}{dx}\left[
\left(\sum_{j=1}^2 u_j\cfrac{d\psi_j}{dx}\right) +
\frac{1}{2}\cfrac{dw_0}{dx}
\left(\sum_{j=1}^4 d_j\cfrac{d\phi_j}{dx}\right)\right]
A_{xx}~dx =
\int_{x_a}^{x_b} \psi_i f~dx + \psi_i(x_a) Q_1 + \psi_i(x_b) Q_4 ~.](../I/m/f8236a4df542cfec46ff2ee99da75b95.png)
![\begin{align}
\sum_{j=1}^{2}
\left[\int_{x_a}^{x_b} A_{xx}\cfrac{d\psi_i}{dx}\cfrac{d\psi_j}{dx}~dx\right]u_j & +
\sum_{j=1}^{4}
\left[\frac{1}{2} \int_{x_a}^{x_b} \left(A_{xx}\cfrac{dw_0}{dx}\right)
\cfrac{d\psi_i}{dx} \cfrac{d\phi_j}{dx}~dx\right]d_j = \\
& \int_{x_a}^{x_b} \psi_i f~dx + \psi_i(x_a) Q_1 + \psi_i(x_b) Q_4 ~.
\end{align}](../I/m/31a01635b1e36366bb5006849b5f2f42.png)
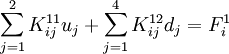
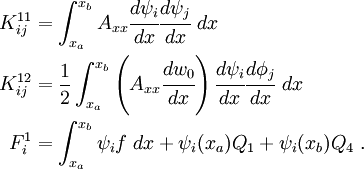
![\begin{align}
\int_{x_a}^{x_b} \left\{\cfrac{d\phi_i}{dx} \right. &
\left[\left(\sum_{j=1}^{2} u_j\cfrac{d\psi_j}{dx}\right) +
\frac{1}{2}\cfrac{dw_0}{dx}
\left(\sum_{j=1}^{4} d_j\cfrac{d\phi_j}{dx}\right)\right]
\cfrac{dw_0}{dx}A_{xx} +
\left.\cfrac{d^2\phi_i}{dx^2}
\left(\sum_{j=1}^{4} d_j \cfrac{d^2\phi_j}{dx^2}\right)D_{xx} \right\}~dx =
\\
& \int_{x_a}^{x_b} \phi_i q~dx +
\phi_i(x_a) Q_2 + \phi_i(x_b) Q_5 +
\cfrac{d\phi_i}{dx}(x_a) Q_3 +
\cfrac{d\phi_i}{dx}(x_b) Q_6
\end{align}](../I/m/5e906b79a63fa1423547bda1a6782c93.png)
![\begin{align}
\sum_{j=1}^{2} \left[ \int_{x_a}^{x_b} \left(A_{xx} \cfrac{dw_0}{dx}\right)
\cfrac{d\phi_i}{dx}\cfrac{d\psi_j}{dx}~dx \right] u_j& +
\sum_{j=1}^{4} \left\{\frac{1}{2}
\int_{x_a}^{x_b} \left[A_{xx} \left(\cfrac{dw_0}{dx}\right)^2\right]
\cfrac{d\phi_i}{dx}\cfrac{d\phi_j}{dx}~dx \right\} d_j\\
& + \sum_{j=1}^{4} \left( \int_{x_a}^{x_b} D_{xx}\cfrac{d^2\phi_i}{dx^2}\cfrac{d^2\phi_j}{dx^2}~dx
\right) d_j =
\\
& \int_{x_a}^{x_b} \phi_i q~dx + \phi_i(x_a) Q_2 + \phi_i(x_b) Q_5 +
\cfrac{d\phi_i}{dx}(x_a) Q_3 + \cfrac{d\phi_i}{dx}(x_b) Q_6
\end{align}](../I/m/a306905654d6749388d3ea63efa754de.png)
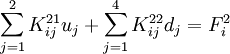
![\begin{align}
K_{ij}^{21} & = \int_{x_a}^{x_b} \left(A_{xx} \cfrac{dw_0}{dx}\right)
\cfrac{d\phi_i}{dx}\cfrac{d\psi_j}{dx}~dx\\
K_{ij}^{22} & = \int_{x_a}^{x_b}\left\{
\frac{1}{2}\left[A_{xx} \left(\cfrac{dw_0}{dx}\right)^2\right]
\cfrac{d\phi_i}{dx}\cfrac{d\phi_j}{dx} +
D_{xx}\cfrac{d^2\phi_i}{dx^2}\cfrac{d^2\phi_j}{dx^2}\right\}~dx \\
F_i^2 & = \int_{x_a}^{x_b} \phi_i q~dx + \phi_i(x_a) Q_2 + \phi_i(x_b) Q_5 +
\cfrac{d\phi_i}{dx}(x_a) Q_3 + \cfrac{d\phi_i}{dx}(x_b) Q_6 ~.
\end{align}](../I/m/287ad4e6d159bd1e9b393dc74555e1d7.png)


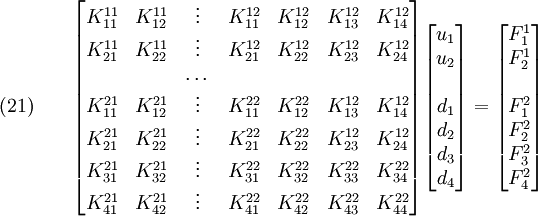
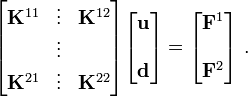
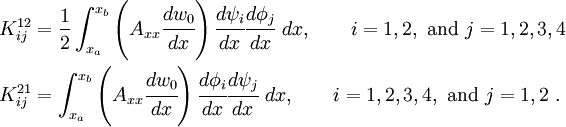
![\begin{align}
\int_{x_a}^{x_b} \left\{\cfrac{d(\delta w_0)}{dx} \right. &
\left[\frac{1}{2}\cfrac{du_0}{dx}+\frac{1}{2}\left(\cfrac{dw_0}{dx}\right)^2+
{\frac{1}{2}\cfrac{du_0}{dx}}\right] \cfrac{dw_0}{dx} A_{xx} +
\left.\cfrac{d^2(\delta w_0)}{dx^2} \left(\cfrac{d^2w_0}{dx^2}\right) D_{xx} \right\}~dx = \\
& \int_{x_a}^{x_b} (\delta w_0) q~dx +
\delta w_0(x_a) Q_2 + \delta w_0(x_b) Q_5 +
\delta \theta(x_a) Q_3 +
\delta \theta(x_b) Q_6 ~.
\end{align}](../I/m/12a87337be20e4071e090ebe92c51a80.png)
![\begin{align}
\int_{x_a}^{x_b} \left\{\cfrac{d\phi_i}{dx} \right. &
\left[\frac{1}{2}\left(\sum_{j=1}^{2} u_j\cfrac{d\psi_j}{dx}\right) +
\frac{1}{2}\cfrac{dw_0}{dx}
\left(\sum_{j=1}^{4} d_j\cfrac{d\phi_j}{dx}\right)
\right]
\cfrac{dw_0}{dx}A_{xx} +
{
\frac{1}{2}\cfrac{d\phi_i}{dx}
\cfrac{du_0}{dx}\left(\sum_{j=1}^{4} d_j\cfrac{d\phi_j}{dx}\right)A_{xx} +
}\\
&\left.\cfrac{d^2\phi_i}{dx^2}
\left(\sum_{j=1}^{4} d_j \cfrac{d^2\phi_j}{dx^2}\right)D_{xx} \right\}~dx =
\\
& \int_{x_a}^{x_b} \phi_i q~dx +
\phi_i(x_a) Q_2 + \phi_i(x_b) Q_5 +
\cfrac{d\phi_i}{dx}(x_a) Q_3 +
\cfrac{d\phi_i}{dx}(x_b) Q_6
\end{align}](../I/m/f7b1b126addac9ddf907db89726712ba.png)
![\begin{align}
\sum_{j=1}^{2} & \left[\frac{1}{2} \int_{x_a}^{x_b} \left(A_{xx} \cfrac{dw_0}{dx}\right)
\cfrac{d\phi_i}{dx}\cfrac{d\psi_j}{dx}~dx \right] u_j +
\sum_{j=1}^{4} \left\{\frac{1}{2}
\int_{x_a}^{x_b} \left[A_{xx} \left(\cfrac{dw_0}{dx}\right)^2\right]
\cfrac{d\phi_i}{dx}\cfrac{d\phi_j}{dx}~dx \right\} d_j + \\
& {
\sum_{j=1}^{4} \left[\frac{1}{2}\int_{x_a}^{x_b} A_{xx}\cfrac{du_0}{dx}\cfrac{d\phi_i}{dx}
\cfrac{d\phi_j}{dx}~dx\right] d_j
}
+ \sum_{j=1}^{4} \left( \int_{x_a}^{x_b} D_{xx}\cfrac{d^2\phi_i}{dx^2}\cfrac{d^2\phi_j}{dx^2}~dx
\right) d_j =
\\
& \int_{x_a}^{x_b} \phi_i q~dx + \phi_i(x_a) Q_2 + \phi_i(x_b) Q_5 +
\cfrac{d\phi_i}{dx}(x_a) Q_3 + \cfrac{d\phi_i}{dx}(x_b) Q_6
\end{align}](../I/m/95b5ad990e86c742c5fcb212e4b7a549.png)
![\begin{align}
K_{ij}^{21} & = \frac{1}{2} \int_{x_a}^{x_b} \left(A_{xx} \cfrac{dw_0}{dx}\right)
\cfrac{d\phi_i}{dx}\cfrac{d\psi_j}{dx}~dx\\
K_{ij}^{22} & = \int_{x_a}^{x_b}\left\{
\frac{1}{2} A_{xx}
\left[\cfrac{du_0}{dx}+\left(\cfrac{dw_0}{dx}\right)^2\right]
\cfrac{d\phi_i}{dx}\cfrac{d\phi_j}{dx} +
D_{xx}\cfrac{d^2\phi_i}{dx^2}\cfrac{d^2\phi_j}{dx^2}\right\}~dx \\
F_i^2 & = \int_{x_a}^{x_b} \phi_i q~dx + \phi_i(x_a) Q_2 + \phi_i(x_b) Q_5 +
\cfrac{d\phi_i}{dx}(x_a) Q_3 + \cfrac{d\phi_i}{dx}(x_b) Q_6 ~.
\end{align}](../I/m/5ed6b66c3083e2d5d337f8eb15a1b5e6.png)
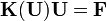
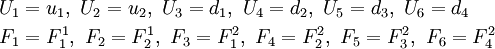
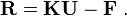
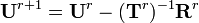
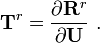
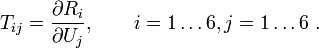
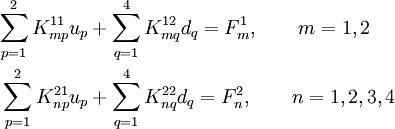
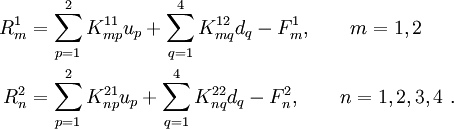
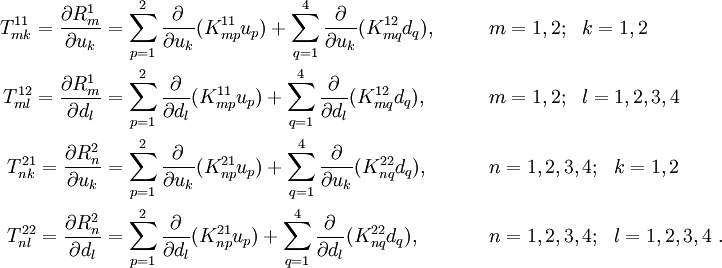
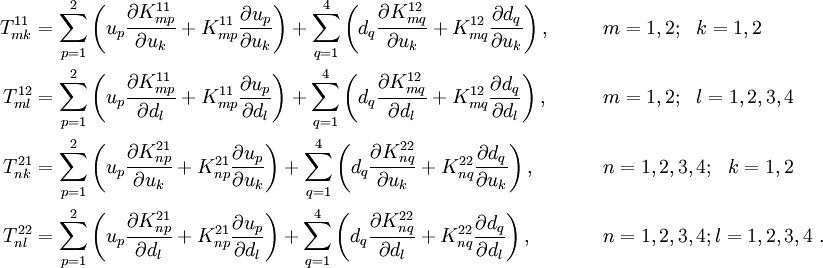
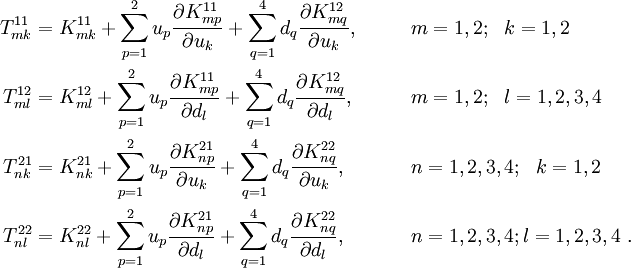
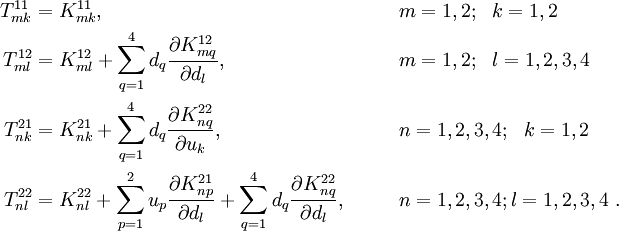
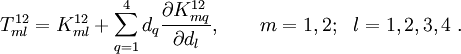
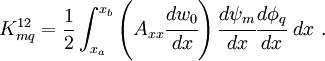
![\begin{align}
\frac{\partial K_{mq}^{12}}{\partial d_l} &=
\frac{1}{2}\int_{x_a}^{x_b}\left[A_{xx}\frac{\partial }{\partial d_l}\left(\cfrac{dw_0}{dx}\right)\right]
\cfrac{d\psi_m}{dx} \cfrac{d\phi_q}{dx}~dx \\
& =
\frac{1}{2}\int_{x_a}^{x_b}\left[A_{xx}\left(\sum_{T=1}^{4}\frac{\partial d_T}{\partial d_l}
\cfrac{d\phi_T}{dx}\right)\right]
\cfrac{d\psi_m}{dx} \cfrac{d\phi_q}{dx}~dx \\
& =
\frac{1}{2}\int_{x_a}^{x_b}\left[A_{xx}\cfrac{d\phi_l}{dx}\right]
\cfrac{d\psi_m}{dx} \cfrac{d\phi_q}{dx}~dx
\end{align}](../I/m/cff53ff92cdd06eec131e4a4a6fcdffc.png)
![\begin{align}
{ T^{12}_{ml}} & = K^{12}_{ml} +
\sum_{q=1}^{4} d_q\left\{
\frac{1}{2}\int_{x_a}^{x_b}\left[A_{xx}\cfrac{d\phi_l}{dx}\right]
\cfrac{d\psi_m}{dx} \cfrac{d\phi_q}{dx}~dx \right\}
\qquad m=1,2; ~~l=1,2,3,4 ~. \\
& = K^{12}_{ml} +
\frac{1}{2}\int_{x_a}^{x_b} A_{xx}\cfrac{d\phi_l}{dx}
\cfrac{d\psi_m}{dx}\left(\sum_{q=1}^{4}d_q\cfrac{d\phi_q}{dx}\right)~dx
\\
& = K^{12}_{ml} +
\frac{1}{2}\int_{x_a}^{x_b} A_{xx}\cfrac{d\phi_l}{dx}
\cfrac{d\psi_m}{dx}\cfrac{dw_0}{dx}~dx\\
& = { 2K^{12}_{ml}} ~.
\end{align}](../I/m/e03a74a03147678c02b03af7034a123f.png)
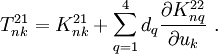
![K_{nq}^{22}= \int_{x_a}^{x_b}\left\{
\frac{1}{2} A_{xx}
\left[\cfrac{du_0}{dx}+\left(\cfrac{dw_0}{dx}\right)^2\right]
\cfrac{d\phi_n}{dx}\cfrac{d\phi_q}{dx} +
D_{xx}\cfrac{d^2\phi_n}{dx^2}\cfrac{d^2\phi_q}{dx^2}\right\}~dx ~.](../I/m/974741cb8bef363561426152cb07dd72.png)
![\begin{align}
\frac{\partial K_{nq}^{22}}{\partial u_k} & = \int_{x_a}^{x_b}
\frac{1}{2} A_{xx}
\left[\sum_{T=1}^{2}\frac{\partial u_T}{\partial u_k}\cfrac{d\psi_T}{dx}+
2\cfrac{dw_0}{dx}\left(\sum_{T=1}^{4}\frac{\partial d_T}{\partial u_k}\cfrac{d\phi_T}{dx}
\right)\right]
\cfrac{d\phi_n}{dx}\cfrac{d\phi_q}{dx}~dx \\
&= \frac{1}{2}\int_{x_a}^{x_b} A_{xx} \cfrac{d\psi_k}{dx}
\cfrac{d\phi_n}{dx}\cfrac{d\phi_q}{dx}~dx \\
\end{align}](../I/m/e1f1ea3667999814fbaaa7e4e04170eb.png)
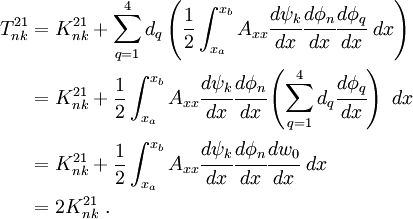
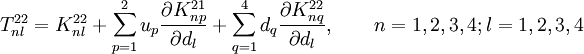
![\begin{align}
\frac{\partial K_{np}^{21}}{\partial d_l} & =
\frac{1}{2} \int_{x_a}^{x_b} \left[A_{xx} \frac{\partial }{\partial d_l}\left(\cfrac{dw_0}{dx}\right)
\right] \cfrac{d\phi_n}{dx}\cfrac{d\psi_p}{dx}~dx\\
& = \frac{1}{2} \int_{x_a}^{x_b} A_{xx}\left[\sum_{T=1}^{4}\frac{\partial d_T}{\partial d_l}\cfrac{d\phi_T}{dx}
\right] \cfrac{d\phi_n}{dx}\cfrac{d\psi_p}{dx}~dx \\
& = \frac{1}{2} \int_{x_a}^{x_b} A_{xx}\cfrac{d\phi_l}{dx}\cfrac{d\phi_n}{dx}
\cfrac{d\psi_p}{dx}~dx
\end{align}](../I/m/ab208d688180d2be4284a6c6242c5a84.png)
![\begin{align}
\frac{\partial K_{nq}^{22}}{\partial d_l} & = \int_{x_a}^{x_b} \frac{1}{2} A_{xx}
\left[\sum_{T=1}^{2}\frac{\partial u_T}{\partial d_l}\cfrac{d\psi_T}{dx}+
2\cfrac{dw_0}{dx}\left(\sum_{T=1}^{4}
\frac{\partial d_T}{\partial d_l}\cfrac{d\phi_T}{dx}\right)\right]
\cfrac{d\phi_n}{dx}\cfrac{d\phi_q}{dx}~dx \\
& = \int_{x_a}^{x_b} A_{xx} \cfrac{dw_0}{dx} \cfrac{d\phi_l}{dx}
\cfrac{d\phi_n}{dx}\cfrac{d\phi_q}{dx}~dx
\end{align}](../I/m/3c06b8e31e932e15ab8ab767f2ed169a.png)
![\begin{align}
{ T^{22}_{nl}} & = K^{22}_{nl} +
\sum_{p=1}^{2} u_p \left[
\frac{1}{2} \int_{x_a}^{x_b} A_{xx}\cfrac{d\phi_l}{dx}\cfrac{d\phi_n}{dx}
\cfrac{d\psi_p}{dx}~dx \right] +
\sum_{q=1}^{4} d_q \left[
\int_{x_a}^{x_b} A_{xx} \cfrac{dw_0}{dx} \cfrac{d\phi_l}{dx}
\cfrac{d\phi_n}{dx}\cfrac{d\phi_q}{dx}~dx \right]\\
& = K^{22}_{nl} +
\frac{1}{2} \int_{x_a}^{x_b} A_{xx}\cfrac{d\phi_l}{dx}\cfrac{d\phi_n}{dx}
\left(\sum_{p=1}^{2} u_p \cfrac{d\psi_p}{dx}\right)~dx+
\int_{x_a}^{x_b} A_{xx} \cfrac{dw_0}{dx} \cfrac{d\phi_l}{dx} \cfrac{d\phi_n}{dx}
\left(\sum_{q=1}^{4} d_q \cfrac{d\phi_q}{dx}\right)~dx\\
& = K^{22}_{nl} +
\frac{1}{2} \int_{x_a}^{x_b} A_{xx}\cfrac{d\phi_l}{dx}\cfrac{d\phi_n}{dx}
\cfrac{du_0}{dx}~dx +
\int_{x_a}^{x_b} A_{xx} \cfrac{dw_0}{dx} \cfrac{d\phi_l}{dx} \cfrac{d\phi_n}{dx}
\cfrac{dw_0}{dx}~dx \\
& = { K^{22}_{nl} +
\frac{1}{2} \int_{x_a}^{x_b} A_{xx}\left[\cfrac{du_0}{dx} +
2\left(\cfrac{dw_0}{dx}\right)^2\right]
\cfrac{d\phi_l}{dx}\cfrac{d\phi_n}{dx}~dx }~.
\end{align}](../I/m/edaea2d32cabb84aa8b96f7f817bfd9d.png)
![\begin{align}
T^{11}_{ij} & = K^{11}_{ij},
& &\qquad i=1,2; ~~j=1,2 \\
T^{12}_{ij} & = 2 K^{12}_{ij},
& & \qquad i=1,2; ~~j=1,2,3,4 \\
T^{21}_{ij} & = 2 K^{21}_{ij},
& & \qquad i=1,2,3,4; ~~j=1,2 \\
T^{22}_{ij} & = K^{22}_{ij} +
\frac{1}{2} \int_{x_a}^{x_b} A_{xx}\left[\cfrac{du_0}{dx} +
2\left(\cfrac{dw_0}{dx}\right)^2\right]
\cfrac{d\phi_i}{dx}\cfrac{d\phi_j}{dx}~dx
& & \qquad i=1,2,3,4; j=1,2,3,4 ~.
\end{align}](../I/m/e88a6f497c875e03e77c28e98119e405.png)