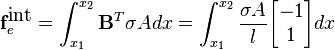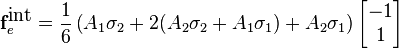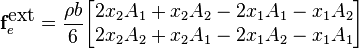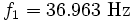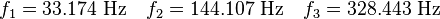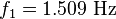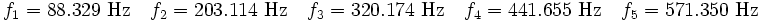Nonlinear finite elements/Homework 9/Solutions
< Nonlinear finite elements < Homework 9Problem 1: Total Lagrangian
Given:
Consider the tapered two-node element shown in Figure 1. The displacement field in the element is linear.
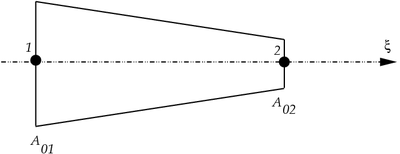 Figure 1. Tapered two-node element. |
The reference (initial) cross-sectional area is
Assume that the nominal (engineering) stress is also linear in the element, i.e.,
Solution
Part 1
Using the total Lagrangian formulation, develop expressions for the internal nodal forces.
The displacement field is given by the linear Lagrange interpolation expressed in terms of the material coordinate.
where 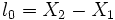 . The strain measure is evaluated in terms of the nodal displacement,
. The strain measure is evaluated in terms of the nodal displacement,
which defines the  matrix to be
matrix to be
The internal nodal forces are then given by the usual relations.
Integrating the above integral with 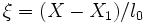 to obtain
to obtain
Part 2
What are the internal nodal forces if the reference area and the nominal stress are constant over the element?
Part 3
Assume that the body force is constant. Develop expressions for the external nodal forces for that case.
The external body forces arising from the body force, 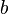 , are obtained by the usual procedure.
, are obtained by the usual procedure.
Part 4
What are the external nodal forces if the reference area and the nominal stress are constant over the element?
Part 5
Develop an expression for the consistent mass matrix for the element.
The element mass matrix is
Part 6
Obtain the lumped (diagonal) mass matrix using the row-sum technique.
Lumped mass matrix is given by
Part 7
Find the natural frequencies of a single element with consistent mass by solving the eigenvalue problem
with
where  is the Young's modulus and
is the Young's modulus and 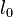 is the initial length of the element.
is the initial length of the element.
The above equation can be rewrite as
which only has a solution if
Solving the above determinant for 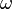 , we have
, we have
Problem 2: Updated Lagrangian
Given:
Consider the tapered two-node element shown in Figure 1.
The current cross-sectional area is
Assume that the Cauchy stress is also linear in the element, i.e.,
Solution
Part 1
Using the updated Lagrangian formulation, develop expressions for the internal nodal forces.
The velocity field is
In term of element coordinates, the velocity field is
The displacement is the time integrals of the velocity,
and since 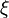 is independent of time
is independent of time
Therefore, since 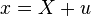
where 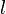 is the current length of the element. For this
element, we can express
is the current length of the element. For this
element, we can express 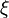 in terms of the Eulerian
coordinates by
in terms of the Eulerian
coordinates by
So 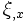 can be obtained directly, instead of
through the inverse of
can be obtained directly, instead of
through the inverse of 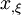 .
.
The 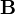 matrix is obtained by the chain rule
matrix is obtained by the chain rule
Using (146) in Handout 13, we have
Integrating the above equation to obtain
Part 2
Assume that the body force is constant. Develop expressions for the external nodal forces for that case.
The external forces are given by
Problem 3: Modal Analysis
Given: Consider the axially loaded bar in problem VM 59 of the ANSYS Verification manual. Assume that the bar is made of Tungsten carbide.
The input file for ANSYS is as shown in VM 59 except the following material properties are used: 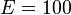 Msi and
Msi and 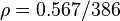 lb
lb s
s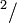 in
in .
.
Solution
Find the fundamental natural frequency of the bar.
Find the first three modal frequencies for a load of 40,000 lbf.
Given:
Consider the stretched circular membrane in problem VM 55 of the ANSYS
Verification manual. Assume that the membrane is made of OFHC (Oxygen-free
High Conductivity) copper.
The input file for ANSYS is as shown in VM 55 except the following material properties are used: 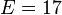 Msi and
Msi and 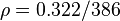 lb
lb s
s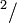 in
in , and the modes are expanded to 5.
, and the modes are expanded to 5.
Solution
Find the fundamental natural frequency of the bar.
Find the first five modal frequencies for a load of 10,000 lbf.
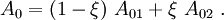
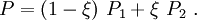
![\mathbf{u}(X,t) =\frac{1}{l_0}[X_2-X\quad X-X_1]
\begin{bmatrix}
u_1(t)\\
u_2(t)
\end{bmatrix}](../I/m/8b209dc48c5ddb03162792ca067e81c5.png)
![\boldsymbol{\varepsilon}(X,t)=u_{,X}=\frac{1}{l_0}[-1\quad 1]
\begin{bmatrix}
u_1(t)\\
u_2(t)
\end{bmatrix}](../I/m/28335070c89b5579f3898cfd11222107.png)
![\mathbf{B}_0=\frac{1}{l_0}[-1\quad 1].](../I/m/37cf4aa8f750570566405a05de7f80cc.png)
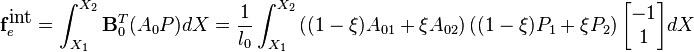
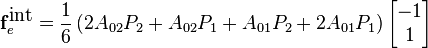
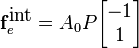
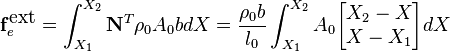
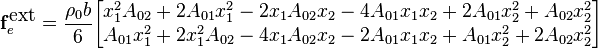
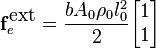
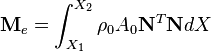
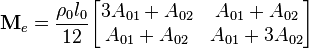
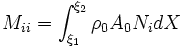
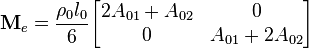
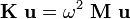
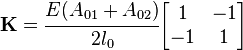
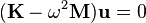
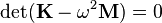
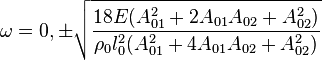
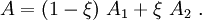
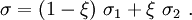
![v(X,t) = \frac{1}{l_0}\left[X_2-X\quad X-X_1\right]
\begin{bmatrix}
v_1(t)\\
v_2(t)
\end{bmatrix}](../I/m/518be492b9d123f9fcc59b9980af5681.png)
![v(\xi,t) = \frac{1}{l_0}\left[1-\xi\quad\xi\right]
\begin{bmatrix}
v_1(t)\\
v_2(t)
\end{bmatrix}\qquad \xi=\frac{X-X_1}{l_0}](../I/m/08a81f2c17e9373c590547ae183f60b1.png)
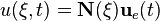
![x(\xi,t)=\mathbf{N}(\xi)\mathbf{x}_e(t)=\left[1-\xi\quad\xi\right]
\begin{bmatrix}
x_1(t)\\
x_2(t)
\end{bmatrix}\qquad \xi_{,\xi}=x_2-x_1=l](../I/m/a974bb1ccde06b953f1b126fa755b3ae.png)
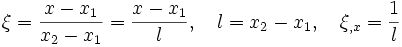
![\mathbf{B}=\mathbf{N}_{,x}=\mathbf{N}_{,\xi}\xi_{,x}=\frac{1}{l}[-1\quad 1]](../I/m/a60f0e9243cda334603c043a78d7f6a2.png)