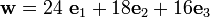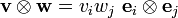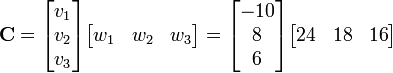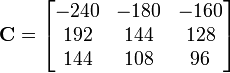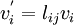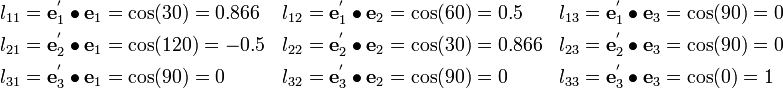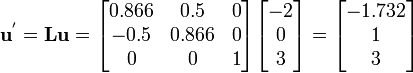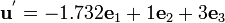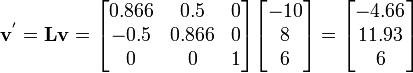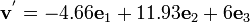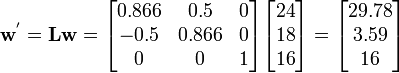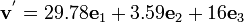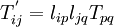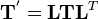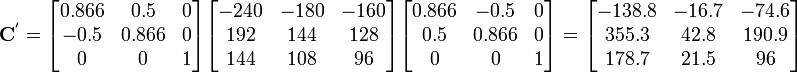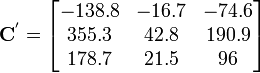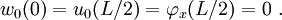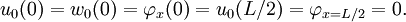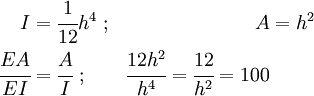Nonlinear finite elements/Homework 7/Solutions
< Nonlinear finite elements < Homework 7Problem 1: Index Notation
Solutions
Part 1
- Determine whether the following expressions are valid in index notation. If valid, identify the free indices and the dummy indices.
1) 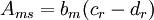
Invalid. The free indices are 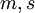 on the LHS and
on the LHS and 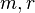 on the RHS.
on the RHS.
2) 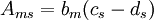
Valid. Both 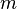 and
and  are free indices.
are free indices.
3) 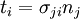
Valid. The free index is 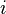 and the dummy index is
and the dummy index is 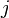 .
.
4) 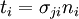
Invalid. The free index is 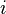 on the LHS and
on the LHS and 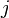 on the RHS.
on the RHS.
5) 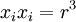
Valid. The dummy index is 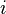 . So the sum is a scalar which is equal to
. So the sum is a scalar which is equal to 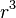 .
.
6) 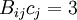
Invalid. There is one free index on the LHS and no free index on the RHS.
Part 2
Show the following:
1) 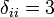
2) 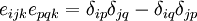
The LHS is
If 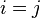 , then we have
, then we have
We get the same result if 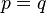 . The only nonzero LHS and RHS occur when
. The only nonzero LHS and RHS occur when 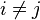 and
and 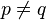 .
.
- Case 1:
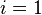 ,
, 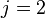 ,
, 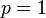 ,
, 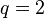 .
.
- Case 2:
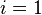 ,
, 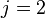 ,
, 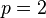 ,
, 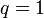 or
or
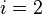 ,
, 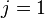 ,
, 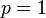 ,
, 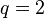 .
.
- Case 3:
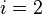 ,
, 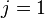 ,
, 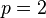 ,
, 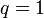 .
.
- Case 4:
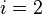 ,
, 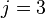 ,
, 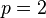 ,
, 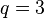 .
.
- Case 5:
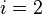 ,
, 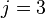 ,
, 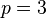 ,
, 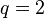 or
or
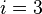 ,
, 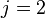 ,
, 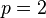 ,
, 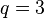 .
.
- Case 6:
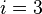 ,
, 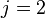 ,
, 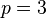 ,
, 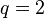 .
.
- Case 7:
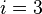 ,
, 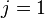 ,
, 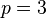 ,
, 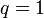 .
.
- Case 8:
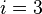 ,
, 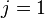 ,
, 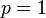 ,
, 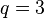 or
or
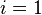 ,
, 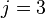 ,
, 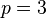 ,
, 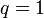 .
.
- Case 9:
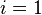 ,
, 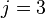 ,
, 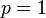 ,
, 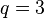 .
.
Hence the 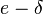 relation is satisfied for all cases.
relation is satisfied for all cases.
3) 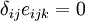
4) 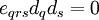
For  ,
,
For 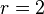 ,
,
For 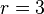 ,
,
Hence shown.
Part 3
The elasticity tensor is given by
where 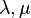 are Lame constants,
are Lame constants, 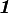 is the second order identity tensor, and
is the second order identity tensor, and  is the fourth-order symmetric identity tensor. The two identity tensors are defined as
is the fourth-order symmetric identity tensor. The two identity tensors are defined as
The stress-strain relation is
Show that the stress-strain relation can be written in index notation as
Write the stress-strain relations in expanded form.
Now, in dyadic notation
Therefore
Similarly,
The stress-strain law becomes
Expanding the left hand side, we get
Therefore,
Problem 2: Rotating Vectors and Tensors
Let (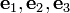 ) be an orthonormal basis. Let
) be an orthonormal basis. Let 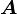 be a second order tensor and
be a second order tensor and 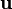 be a vector with components
be a vector with components
Solution
Part 1
Write out 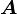 and
and 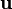 in matrix notation.
in matrix notation.
Part 2
Find the components of the vector 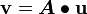 in the basis (
in the basis (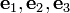 ).
).
The components of 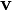 are
are
Therefore
Part 3
Find the components of the vector 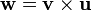 in the basis (
in the basis (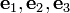 ).
).
The cross product is given by
Therefore,
Part 4
Find the components of the tensor 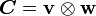 in the orthonormal basis.
in the orthonormal basis.
The tensor product is given by
Hence, in matrix notation
Part 5
Rotate the basis clockwise by 30 degrees around the 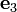 direction. Find the components of
direction. Find the components of 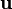 ,
, 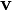 ,
, 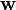 , and
, and 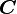 in the rotated basis.
in the rotated basis.
The vector transformation rule is
where 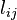 are the direction cosines.
are the direction cosines.
In this case, the direction cosines are
Therefore,
Similarly,
Also,
From the handout from Slaughter's book, the tensor transformation rule is
where 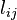 are the direction cosines.
are the direction cosines.
In matrix form,
Therefore the components of 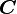 in the rotated basis are give by
in the rotated basis are give by
Problem 3: More Beams
Part A
Consider a beam of length 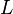 = 100 in., cross-section 1 in.
= 100 in., cross-section 1 in. 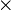 1 in., and subjected to a uniformly distributed transverse load
1 in., and subjected to a uniformly distributed transverse load 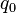 lbf/in. Model one half of the beam using symmetry considerations.
lbf/in. Model one half of the beam using symmetry considerations.
Part 1
Hinged-Hinged Beam
The boundary conditions are
Compute a plot similar to that shown in Figure 4.3.4 for this case using Beam188 elements. What do you observe?
The result is shown in Table 1.
| Table 1. Deflections of a hinged-hinged beam | |
|---|---|
| Load | 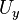 at at 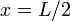 |
| 1 | -0.520746 |
| 2 | -1.04086 |
| 3 | -1.55922 |
| 4 | -2.07510 |
| 5 | -2.58768 |
| 6 | -3.09622 |
| 7 | -3.60000 |
| 8 | -4.09835 |
| 9 | -4.59065 |
| 10 | -5.07636 |
Part 2
Clamped-Clamped Beam
The boundary conditions are
Compute a plot for this case using Beam188 elements. Comment on your plot.
The result is shown in Table 2.
| Table 2. Deflections of a clamped-clamped beam | |
|---|---|
| Load | 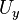 at at 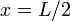 |
| 1 | -0.103456 |
| 2 | -0.202476 |
| 3 | -0.294220 |
| 4 | -0.377753 |
| 5 | -0.453387 |
| 6 | -0.521968 |
| 7 | -0.584455 |
| 8 | -0.644185 |
| 9 | -0.696440 |
| 10 | -0.745243 |
Listed below is the ANSYS input code for Problem 3A.1 and 3A.2.
/prep7
b = 1
h = 1
et,1,188
sectype,1,beam,rect
secdata,b,h
MP,EX,1,30e6
MP,PRXY,1,0.3
K,1,0,0,0
K,2,50,0,0
k,3,0,50,0
L,1,2,50
latt,1,,1,,3,3,1
LMESH,ALL
!change this section to d,1,all,0 for Problem 3A.2
d,1,uy,0
d,1,uz,0
d,2,rotz,0
nsel,all
sfbeam,all,,pres,10
fini
/solu
nlgeom,on
autots,on
nsubst,10,100,10
outres,all,all
solve
finish
Part B
Part 1
Simulate the unrolling of a cantilever beam from Section 4.1.1 of Ibrahimbegovic (1995) and compare your results with the results shown in the paper.
The result is shown in Table 3.
| Table 3. Cantilever free-end displacement components | |||
|---|---|---|---|
| Load | 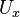 |
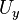 |
Rotation |
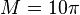 |
-0.040666 | 6.3205 | -3.1287 |
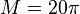 |
9.9578 | 0.12729 | -6.2577 |
The deformation plots are shown in Figure 4 and 5.
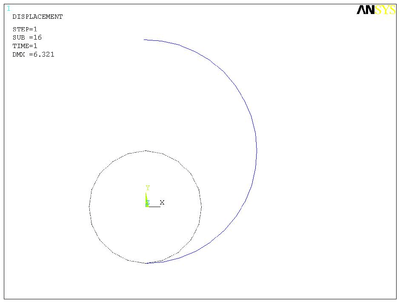 Figure 4. Deformed shape under 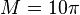 for Problem 3B.1. for Problem 3B.1. |
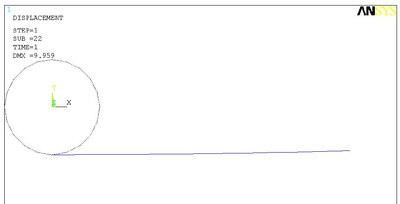 Figure 5. Deformed shape under 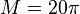 for Problem 3B.1. for Problem 3B.1. |
The ANSYS input code for this problem is listed below.
/prep7
et,1,beam188
sectype,1,beam,rect
secdata,1,1
mp,ex,1,1200
mp,prxy,1,0
l = 10
pi = 4*atan(1)
r = L/2/pi
K,1,0,-r
K,2,-r,0
K,3,0,r
K,4,r,0
K,5,0,-r
k,6,0,0,10
k,7,0,0,0
larc,1,2,7,r,5
larc,2,3,7,r,5
larc,3,4,7,r,5
larc,4,5,7,r,5
latt,1,,1,,6,6,1
lmesh,all
dk,5,all,0
fk,1,mz,-20*pi
/solu
nlgeom,on
cnvtol,f,5,0.001
outres,all,all
arclen,on
nsubst,100
solve
fini
Part 2
Simulate the clamped-hinged deep circular arch from Example 7.3 of Simo and Vu Quoc (1986) and compare you results with the results shown in the paper.
The inputs are: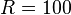 ,
, 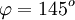 ,
, 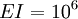 , and
, and 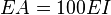 . We assume a square cross section. Then
. We assume a square cross section. Then
Therefore, 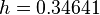 .
.
The deformed shape (unconverged) for a load of 905 is shown in Figure 6.
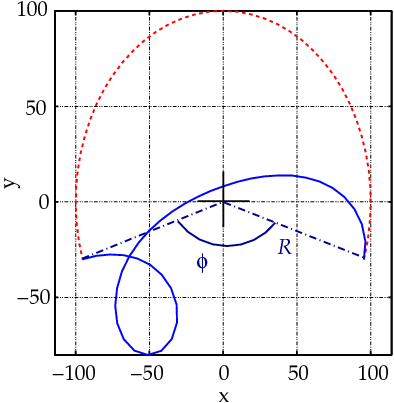 Figure 6. Deformed shape of arch. |
The load-displacement curve (up to the last converged solution) is shown in Figure 7.
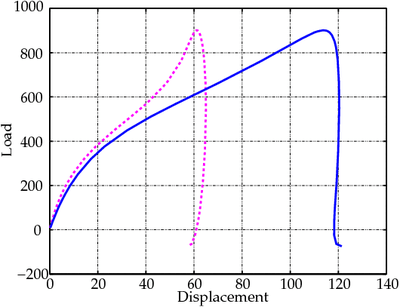 Figure 7. Load-displacement plot for circular arch. |
The buckling load is 900.925 compared to 905.28 in Simo and Vu Quoc.
The ANSYS file use for the calculations is shown below.
/prep7
!*
!* Total load
!*
load = 905.0
!*
!* Element type
!*
et,1,beam188
keyopt,1,1,0
keyopt,1,2,0
keyopt,1,3,0
keyopt,1,4,0
keyopt,1,6,0
keyopt,1,7,0
keyopt,1,8,0
keyopt,1,9,0
keyopt,1,10,0
keyopt,1,11,0
keyopt,1,12,0
!*
!* Beam cross-section type
!*
sectype, 1, beam, rect, , 0
secoffset, cent
secdata, 0.34641, 0.34641, 0,0,0,0,0,0,0,0
!*
!* Material properties
!*
mptemp,,,,,,,,
mptemp,1,0
mpdata,ex,1,,8.3e8
mpdata,prxy,1,,0.33
!*
!* Keypoints
!*
k, 1, 0.000, 0.000, 0.000
k, 2, -95.372, -30.071, 0.000
k ,3, 95.372, -30.071, 0.000
k ,4, 0.000, 100.000, 0.000
!*
!* Arcs
!*
larc,3,4,1,100,
larc,4,2,1,100,
!*
!* Element size = 20 elements per arc
!*
lesize,all, , ,20, ,1, , ,1,
!*
!* Mesh the arcs
!*
lmesh, all
!*
!* Plot the nodes
!*
nplot
/pnum,node,1
/number,0
/replot
!*
!* Apply displacement BCs
!*
!* Hinged end
!*
d, 22, ux, 0
d, 22, uy, 0
d, 22, uz, 0
!*
!* Clamped end
!*
d, 1, all, 0
!*
!* Apply load
!*
f, 2, fy, -load
finish
!*
!* Solve
!*
/solu
antype, static
nlgeom, on
!autots, on
!solcontrol, on
!*
!* Load step 1
!*
time, 1.0
! f, 2, fy, -load
nsubst,100,0,0
kbc, 0
neqit, 100
outres, ,1
arclen,on,100.0,0.0
lswrite
solve
finish
!*
!* See solution
!*
/post26
!*
!* Save solution in variables 2 and 3
!*
nsol, 2, 2, u, x ! Save ux at node 2
nsol, 3, 2, u, y ! Save uy at node 2
!*
!* Scale solution
!*
prod, 4, 1, , , Load, , ,load ! Scale time to get load
prod, 5, 2, , , , , ,-1 ! Make disp +ve
prod, 6, 3, , , , , ,-1 ! Make disp +ve
prvar, 4, 5, 6 ! Print load, ux, uy
!*
!* Plot solution
!*
/axlab, x, Deflection
/axlab, y, Load
/grid, 1
xvar, 5
plvar, 4 ! plot ux vs load
/noerase
xvar, 6
plvar, 4 ! plot uy vs load
/erase
Here is another version of solution to this problem.
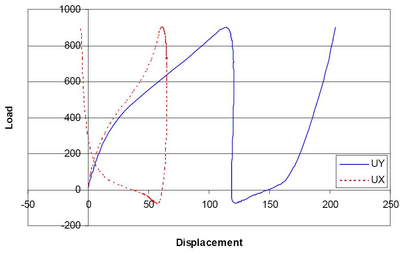 Figure 8. Force-displacement diagram for Problem 3B.2. |
 Figure 9. Shape deformation at the last load step for Problem 3B.2. |
The ANSYS input code for Problem 3B.2 is listed below.
/prep7
A = 1
I = A/100
E = 1e6/I
nu = 0.3
et,1,beam188 ! Element type - BEAM188
sectype,1,beam,asec
secdata,A,I,,I,,2*I
mp,ex,1,E
mp,prxy,1,nu
pi = 4*atan(1)
phi = 35/2/180*pi
x = 100*cos(phi)
y = 100*sin(phi)
k,1,0,0,0
k,2,x,-y,0
k,3,0,100,0
k,4,-x,-y
k,5,0,0,100
larc,2,3,1,100
larc,3,4,1,100
latt,1,,1,,5,5,1
lesize,all,,,40
lmesh,all
dk,2,all,0
dk,4,ux,0
dk,4,uy,0
dk,4,uz,0
fk,3,fy,-900
/solu
nlgeom,on
nsubst,100,0,0
outres,all,all
arclen,on
solve
finish
Part 3
Simulate the buckling of a hinged right-angle frame under both fixed and follower loads from Example 7.4 of Simo and Vu Quoc (1986) and compare your results with those shown in the paper.
The force-displacement diagram is shown in Figure 10. The deformation is illustrated in Figure 11 and 12.
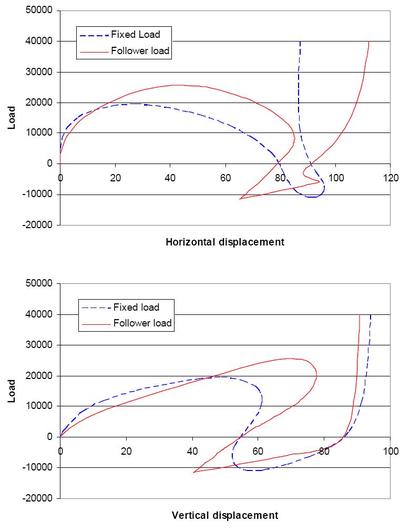 Figure 10. Force-displacement diagram for Problem 3B.3. |
 Figure 11. Deformation (fixed load) at the last load step for Problem 3B.3. |
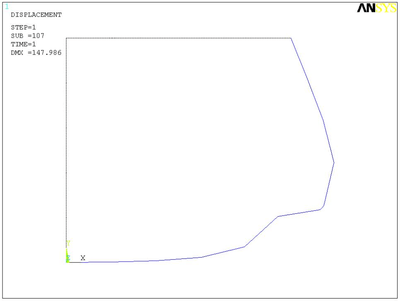 Figure 12. Force-displacement diagram (follower load) for Problem 3B.3. |
The ANSYS input code for Problem 3B.3 is listed below.
/prep7
et,1,188
E = 7.2e6
I = 2
A = 6
sectype,1,beam,asec
secdata,A,I,,I,,2*I
mp,ex,1,7.2e6
mp,prxy,1,0.3
k,1,0,0,0
k,2,0,120,0
k,3,23,120,0
k,4,26,120,0
k,5,120,120,0
k,6,200,0,0
k,7,0,200,0
l,1,2,5
l,2,3,1
l,3,4,2
l,4,5,4
latt,1,,1,,6,6,1
lmesh,1
latt,1,,1,,7,7,1
lmesh,2,4
d,1,ux,0
d,1,uy,0
d,1,uz,0
d,18,ux,0
d,18,uy,0
d,18,uz,0
esel,s,elem,,7,8
!replace the line below with f,15,fy,-40000 for fixed load
sfbeam,all,,pres,40000/2
esel,all
fini
/solu
nlgeom,on
outres,all,all
arclen,on
nsubst,200
solve
fini
Warning: The arc length method no longer converges with Ansys 13. Try using the stabilization option instead of arclen, on:
stabilize, constant, energy, 0.001, anytime, 0
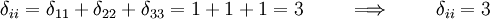
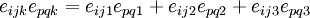
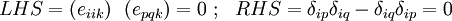
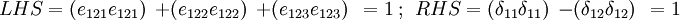
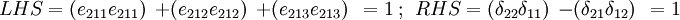
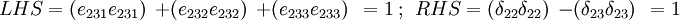
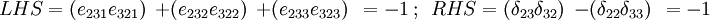
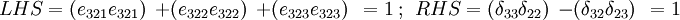
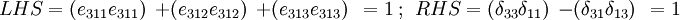
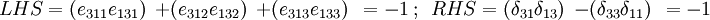
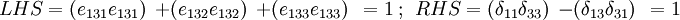
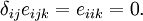
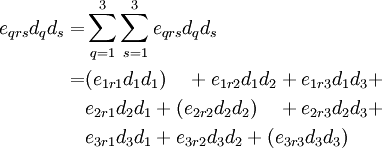
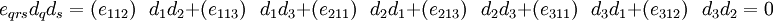
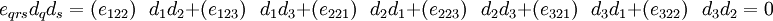
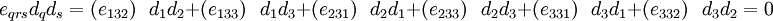
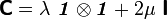
![\begin{align}
\boldsymbol{\mathit{1}} & = \delta_{ij}~\mathbf{e}_i\otimes\mathbf{e}_j \\
\boldsymbol{\mathsf{I}} & = \frac{1}{2}[\delta_{ik}\delta_{jl} + \delta_{il}\delta_{jk}]~
\mathbf{e}_i\otimes\mathbf{e}_j\otimes\mathbf{e}_k\otimes\mathbf{e}_l
\end{align}](../I/m/d16b42b7e1c1288ae3ccce9fa7db1f1c.png)
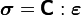
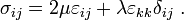
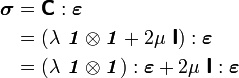
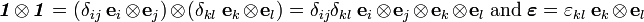
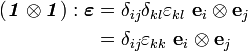
![\begin{align}
\boldsymbol{\mathsf{I}}:\boldsymbol{\varepsilon} & = \left(
\frac{1}{2}[\delta_{ik}\delta_{jl} + \delta_{il}\delta_{jk}]
\varepsilon_{kl}\right)~
\mathbf{e}_i\otimes\mathbf{e}_j \\
& = \frac{1}{2}\left(\delta_{ik}\varepsilon_{kj} + \delta_{il}\varepsilon_{jl}\right)~
\mathbf{e}_i\otimes\mathbf{e}_j \\
& = \frac{1}{2}\left(\varepsilon_{ij} + \varepsilon_{ji}\right)~\mathbf{e}_i\otimes\mathbf{e}_j \\
& = \varepsilon_{ij}~ \mathbf{e}_i\otimes\mathbf{e}_j \qquad \text{(symmetry)}
\end{align}](../I/m/17b389756ca326f3d28193971f1e9cc4.png)
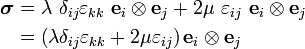
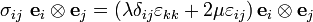
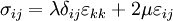
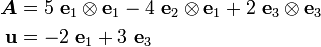
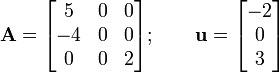
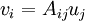
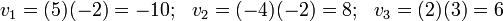
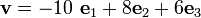
![\mathbf{w} = \mathbf{v}\times\mathbf{u} =
\begin{vmatrix}
\mathbf{e}_1 & \mathbf{e}_2 & \mathbf{e}_3 \\
v_1 & v_2 & v_3 \\
u_1 & u_2 & u_3
\end{vmatrix} =
\begin{vmatrix}
\mathbf{e}_1 & \mathbf{e}_2 & \mathbf{e}_3 \\
-10 & 8 & 6 \\
-2 & 0 & 3
\end{vmatrix} = (8)(3)\mathbf{e}_1 - [(-10)(3)-(6)(-2)]\mathbf{e}_2 -
(8)(-2)\mathbf{e}_3](../I/m/80f257f79469a83d75b0b133cf5d4fbd.png)