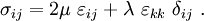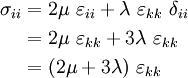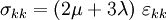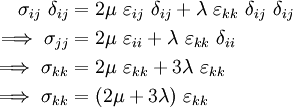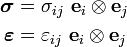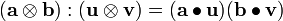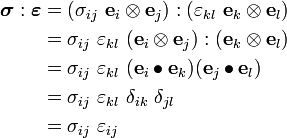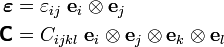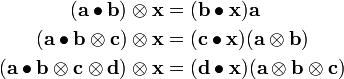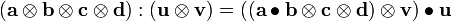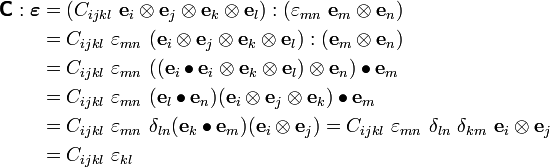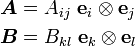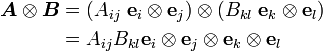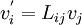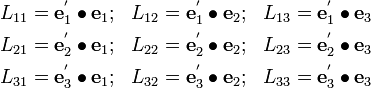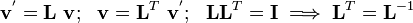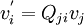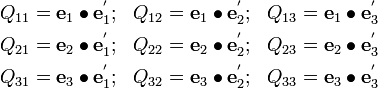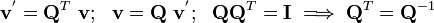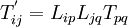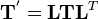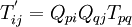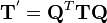Nonlinear finite elements/Homework 7/Hints

< Nonlinear finite elements < Homework 7

Hints 1: Index notation

Index notation:

\sigma_{ij} = 2\mu~\varepsilon_{ij} + \lambda~\varepsilon_{kk}~\delta_{ij}~.

If j=i

\begin{align} \sigma_{ii} & = 2\mu~\varepsilon_{ii} + \lambda~\varepsilon_{kk}~\delta_{ii} \\ & = 2\mu~\varepsilon_{kk} + 3\lambda~\varepsilon_{kk} \\ & = (2\mu + 3\lambda)~\varepsilon_{kk} \end{align}
\sigma_{kk} = (2\mu + 3\lambda)~\varepsilon_{kk}

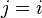
Dummy indices are replaceable.

Hint 2: Index notation

Index notation:

\sigma_{ij} = 2\mu~\varepsilon_{ij} + \lambda~\varepsilon_{kk}~\delta_{ij}~.

Multiply by 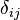\delta_{ij}:

\begin{align} \sigma_{ij}~\delta_{ij} & = 2\mu~\varepsilon_{ij}~\delta_{ij} + \lambda~\varepsilon_{kk}~\delta_{ij}~\delta_{ij}\\ \implies \sigma_{jj}& = 2\mu~\varepsilon_{ii} + \lambda~\varepsilon_{kk}~\delta_{ii}\\ \implies \sigma_{kk}& = 2\mu~\varepsilon_{kk} + 3\lambda~\varepsilon_{kk} \\ \implies \sigma_{kk}& = (2\mu + 3\lambda)~\varepsilon_{kk} \end{align}

Multiplication by 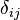\delta_{ij} leads to replacement of one index.

A_{ij}~\delta_{kl} = ? \qquad A_{ij}~\delta{jl} = ?

Hint 3: Index notation

Index notation:

\begin{align} \boldsymbol{\sigma} & =\sigma_{ij}~\mathbf{e}_i\otimes\mathbf{e}_j \\ \boldsymbol{\varepsilon} & =\varepsilon_{ij}~\mathbf{e}_i\otimes\mathbf{e}_j \end{align}

From the definition of dyadic product, we can show

\begin{align} (\mathbf{a}\otimes\mathbf{b}):(\mathbf{u}\otimes\mathbf{v}) & = (\mathbf{a}\bullet\mathbf{u})(\mathbf{b}\bullet\mathbf{v}) \end{align}

Contraction gives:

\begin{align} \boldsymbol{\sigma}:\boldsymbol{\varepsilon} & = (\sigma_{ij}~\mathbf{e}_i\otimes\mathbf{e}_j): (\varepsilon_{kl}~\mathbf{e}_k\otimes\mathbf{e}_l) \\ & = \sigma_{ij}~\varepsilon_{kl}~(\mathbf{e}_i\otimes\mathbf{e}_j): (\mathbf{e}_k\otimes\mathbf{e}_l) \\ & = \sigma_{ij}~\varepsilon_{kl}~ (\mathbf{e}_i\bullet\mathbf{e}_k)(\mathbf{e}_j\bullet\mathbf{e}_l) \\ & = \sigma_{ij}~\varepsilon_{kl}~\delta_{ik}~\delta_{jl} \\ & = \sigma_{ij}~\varepsilon_{ij} \end{align}

Hint 4: Tensor product

Index notation:

\begin{align} \boldsymbol{\varepsilon} & =\varepsilon_{ij}~\mathbf{e}_i\otimes\mathbf{e}_j \\ \boldsymbol{\mathsf{C}} & = C_{ijkl}~\mathbf{e}_i\otimes\mathbf{e}_j\otimes\mathbf{e}_k\otimes\mathbf{e}_l \end{align}

Definition of dyadics products:

\begin{align} (\mathbf{a}\bullet\mathbf{b})\otimes\mathbf{x} & = (\mathbf{b}\bullet\mathbf{x})\mathbf{a} \\ (\mathbf{a}\bullet\mathbf{b}\otimes\mathbf{c})\otimes\mathbf{x} & = (\mathbf{c}\bullet\mathbf{x}) (\mathbf{a}\otimes\mathbf{b}) \\ (\mathbf{a}\bullet\mathbf{b}\otimes\mathbf{c}\otimes\mathbf{d})\otimes\mathbf{x} & = (\mathbf{d}\bullet\mathbf{x}) (\mathbf{a}\otimes\mathbf{b}\otimes\mathbf{c}) \end{align}

We can show that

\begin{align} (\mathbf{a}\otimes\mathbf{b}\otimes\mathbf{c}\otimes\mathbf{d}):(\mathbf{u}\otimes\mathbf{v}) & = ((\mathbf{a}\bullet\mathbf{b}\otimes\mathbf{c}\otimes\mathbf{d})\otimes\mathbf{v})\bullet\mathbf{u} \end{align}

Contraction gives:

\begin{align} \boldsymbol{\mathsf{C}}:\boldsymbol{\varepsilon} & = (C_{ijkl}~\mathbf{e}_i\otimes\mathbf{e}_j \otimes \mathbf{e}_k\otimes\mathbf{e}_l): (\varepsilon_{mn}~\mathbf{e}_m\otimes\mathbf{e}_n) \\ & = C_{ijkl}~\varepsilon_{mn}~(\mathbf{e}_i\otimes\mathbf{e}_j \otimes \mathbf{e}_k\otimes\mathbf{e}_l):(\mathbf{e}_m\otimes\mathbf{e}_n) \\ & = C_{ijkl}~\varepsilon_{mn}~ ((\mathbf{e}_i\bullet\mathbf{e}_i\otimes\mathbf{e}_k\otimes\mathbf{e}_l)\otimes\mathbf{e}_n) \bullet\mathbf{e}_m \\ & = C_{ijkl}~\varepsilon_{mn}~ (\mathbf{e}_l\bullet\mathbf{e}_n)(\mathbf{e}_i\otimes\mathbf{e}_j\otimes\mathbf{e}_k) \bullet\mathbf{e}_m \\ & = C_{ijkl}~\varepsilon_{mn}~\delta_{ln} (\mathbf{e}_k\bullet\mathbf{e}_m)(\mathbf{e}_i\otimes\mathbf{e}_j) = C_{ijkl}~\varepsilon_{mn}~\delta_{ln}~\delta_{km}~\mathbf{e}_i\otimes\mathbf{e}_j \\ & = C_{ijkl}~\varepsilon_{kl} \end{align}

Hint 5 : Tensor product

Tensor Product of two tensors:

\begin{align} \boldsymbol{A} & =A_{ij}~\mathbf{e}_i\otimes\mathbf{e}_j \\ \boldsymbol{B} & =B_{kl}~\mathbf{e}_k\otimes\mathbf{e}_l \end{align}

Tensor product:

\begin{align} \boldsymbol{A}\otimes\boldsymbol{B} & = (A_{ij}~\mathbf{e}_i\otimes\mathbf{e}_j) \otimes (B_{kl}~\mathbf{e}_k\otimes\mathbf{e}_l) \\ & = A_{ij} B_{kl} \mathbf{e}_i\otimes\mathbf{e}_j \otimes \mathbf{e}_k\otimes\mathbf{e}_l \end{align}

Hint 6: Vector transformations

Change of basis: Vector transformation rule

v^{'}_i = L_{ij} v_j

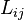L_{ij} are the direction cosines.

\begin{align} L_{11} & = \mathbf{e}_1^{'}\bullet\mathbf{e}_1; & L_{12} & = \mathbf{e}_1^{'}\bullet\mathbf{e}_2; & L_{13} & = \mathbf{e}_1^{'}\bullet\mathbf{e}_3 \\ L_{21} & = \mathbf{e}_2^{'}\bullet\mathbf{e}_1; & L_{22} & = \mathbf{e}_2^{'}\bullet\mathbf{e}_2; & L_{23} & = \mathbf{e}_2^{'}\bullet\mathbf{e}_3 \\ L_{31} & = \mathbf{e}_3^{'}\bullet\mathbf{e}_1; & L_{32} & = \mathbf{e}_3^{'}\bullet\mathbf{e}_2; & L_{33} & = \mathbf{e}_3^{'}\bullet\mathbf{e}_3 \end{align}

In matrix form

\mathbf{v}^{'} = \mathbf{L}~\mathbf{v}; ~~ \mathbf{v} = \mathbf{L}^T~\mathbf{v}^{'}; ~~ \mathbf{L}\mathbf{L}^T = \mathbf{I} \implies \mathbf{L}^T = \mathbf{L}^{-1}

Other common form: Vector transformation rule

v^{'}_i = Q_{ji} v_j
\begin{align} Q_{11} & = \mathbf{e}_1\bullet\mathbf{e}_1^{'}; & Q_{12} & = \mathbf{e}_1\bullet\mathbf{e}_2^{'}; & Q_{13} & = \mathbf{e}_1\bullet\mathbf{e}_3^{'} \\ Q_{21} & = \mathbf{e}_2\bullet\mathbf{e}_1^{'}; & Q_{22} & = \mathbf{e}_2\bullet\mathbf{e}_2^{'}; & Q_{23} & = \mathbf{e}_2\bullet\mathbf{e}_3^{'} \\ Q_{31} & = \mathbf{e}_3\bullet\mathbf{e}_1^{'}; & Q_{32} & = \mathbf{e}_3\bullet\mathbf{e}_2^{'}; & Q_{33} & = \mathbf{e}_3\bullet\mathbf{e}_3^{'} \end{align}

In matrix form

\mathbf{v}^{'} = \mathbf{Q}^T~\mathbf{v}; ~~ \mathbf{v} = \mathbf{Q}~\mathbf{v}^{'}; ~~\mathbf{Q}\mathbf{Q}^T = \mathbf{I} \implies \mathbf{Q}^T = \mathbf{Q}^{-1}

Hint 7: Tensor transformations

Change of basis: Tensor transformation rule

T^{'}_{ij} = L_{ip} L_{jq} T_{pq}

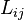where L_{ij} are the direction cosines.

In matrix form,

\mathbf{T}^{'} = \mathbf{L} \mathbf{T} \mathbf{L}^{T}

Other common form

T^{'}_{ij} = Q_{pi} Q_{qj} T_{pq}

In matrix form,

\mathbf{T}^{'} = \mathbf{Q}^T \mathbf{T} \mathbf{Q}
This article is issued from Wikiversity - version of the Tuesday, January 08, 2008. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.