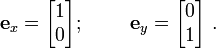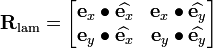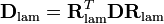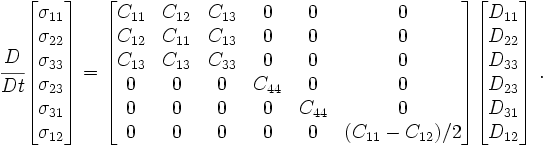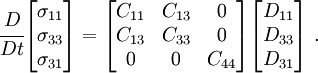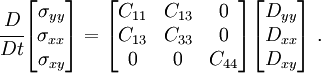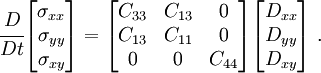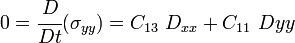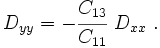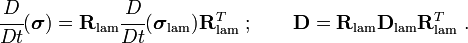Nonlinear finite elements/Homework 6/Hints
< Nonlinear finite elements < Homework 6Hints for Homework 6: Problem 1: Section 8
Use Maple to reduce your manual labor.
The problem becomes easier to solve if we consider numerical values of the parameters. Let the local nodes numbers of element  be
be  for node
for node 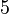 , and
, and 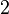 for node
for node 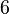 .
.
Let us assume that the beam is divided into six equal sectors. Then,
Let 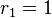 and
and 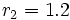 . Since the blue point is midway between the two,
. Since the blue point is midway between the two, 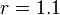 .
.
Also, let the components of the stiffness matrix of the composite be
Let the velocities for nodes 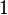 and
and 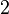 of the element be
of the element be
The  and
and 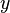 coordinates of the master and slave nodes are
coordinates of the master and slave nodes are
Since there are two master nodes in an element, the parent element is a four-noded quad with shape functions
The isoparametric map is
Therefore, the derivatives with respect to 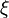 are
are
Since the blue point is at the center of the element, the values of 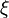 and
and 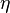 at that point are zero.
Therefore,
at that point are zero.
Therefore,
The local laminar basis vector 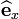 is given by
is given by
The laminar basis vector 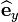 is given by
is given by
To compute the velocity gradient, we have to find the velocities at the slave nodes using the relation
For master node 1 of the element (global node 5), the velocities of the slave nodes are
For master node 2 of the element (global node 6), the velocities of the slave nodes are
The interpolated velocity within the element is given by
The velocity gradient is given by
The velocities are given in terms of the parent element coordinates (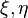 ). We have to convert them to the (
). We have to convert them to the (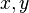 ) system in order to compute the velocity gradient. To do that we recall that
) system in order to compute the velocity gradient. To do that we recall that
In matrix form
and
Therefore,
The rate of deformation is given by
The global base vectors are
Therefore, the rotation matrix is
Therefore, the components of the rate of deformation tensor with respect to the laminar coordinate system are
The rate constitutive relation of the material is given by
Since the problem is a 2-D one, the reduced constitutive equation is
The laminar  -direction maps to the composite
-direction maps to the composite 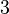 -direction and the laminar
-direction and the laminar 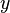 -directions maps to the composite
-directions maps to the composite 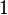 -direction. Hence the constitutive equation can be written as
-direction. Hence the constitutive equation can be written as
Rearranging,
The plane stress condition requires that 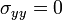 in the laminar coordinate system. We assume that the rate of
in the laminar coordinate system. We assume that the rate of 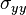 is also zero. In that case, we get
is also zero. In that case, we get
or,
To get the global stress rate and rate of deformation, we have to rotate the components to the global basis using
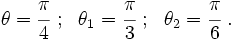
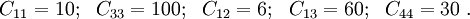
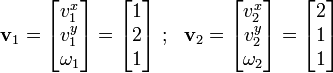
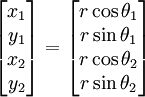
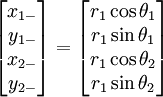
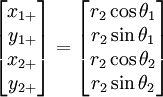
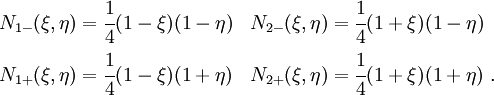
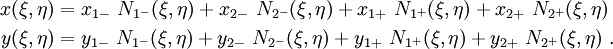
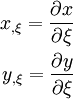
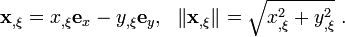
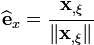
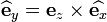
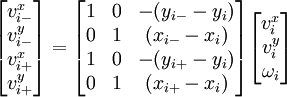
![\begin{align}
\mathbf{v}(\boldsymbol{\xi}, t) & = \cfrac{D}{Dt}[\mathbf{x}(\boldsymbol{\xi},t)] \\
& =
\sum_{i- = 1}^2 \frac{\partial }{\partial t}[\mathbf{x}_{i-}(t)]~N_{i^-}(\xi,\eta) +
\sum_{i+ = 1}^2 \frac{\partial }{\partial t}[\mathbf{x}_{i+}(t)]~N_{i^+}(\xi,\eta)\\
& = \sum_{i- = 1}^2 \mathbf{v}_{i-}(t)~N_{i-}(\xi,\eta) +
\sum_{i+ = 1}^2 \mathbf{v}_{i+}(t)~N_{i+}(\xi,\eta) ~.
\end{align}](../I/m/d9011a658fb6e104a874689e6d5d8ea4.png)
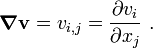
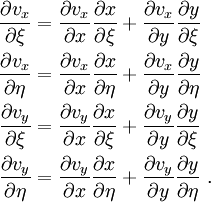
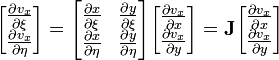

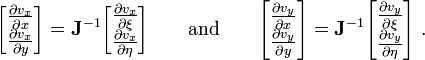
![\boldsymbol{D} = \frac{1}{2}[\boldsymbol{\nabla} \mathbf{v} + (\boldsymbol{\nabla} \mathbf{v})^T] ~.](../I/m/e79076c0e4e642bdea962ebf4be11432.png)