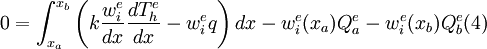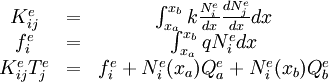Nonlinear finite elements/Homework 2/Solutions
< Nonlinear finite elements < Homework 2Problem 1: Classification of PDEs
Given:
Solution
Part 1
What physical processes do the two PDEs model?
Equation (1) models the one dimensional heat problem where 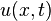 represents temperature at
represents temperature at  at time
at time 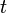 and
and 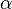 represents the thermal diffusivity.
represents the thermal diffusivity.
Equation (2) models the transverse vibrations of a beam. The variable 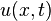 represents the displacement of the point on the beam corresponding to position
represents the displacement of the point on the beam corresponding to position  at time
at time 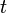 .
. 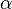 is
is 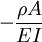 where
where  is Young's modulus,
is Young's modulus, 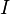 is area moment of inertia,
is area moment of inertia, 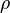 is mass density, and
is mass density, and 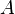 is area of cross section.
is area of cross section.
Part 2
Write out the PDEs in elementary partial differential notation
Part 3
Determine whether the PDEs are elliptic, hyperbolic, or parabolic. Show how you arrived at your classification.
Equation (1) is parabolic for all values of 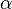 .
.
We can see why by writing it out in the form given in the notes on Partial differential equations.
Hence, we have  ,
,  ,
,  ,
,  ,
, 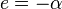 ,
, 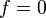 , and
, and 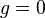 . Therefore,
. Therefore,
Equation (2) is hyperbolic for positive values of 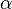 , parabolic when
, parabolic when 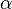 is zero, and elliptic when
is zero, and elliptic when 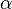 is less than zero.
is less than zero.
Problem 2: Models of Physical Problems
Given:
Solution
- Heat transfer: :
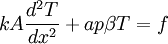
- Flow through porous medium: :
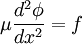
- Flow through pipe: :
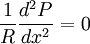
- Flow of viscous fluids: :
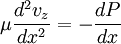
- Elastic cables: :
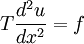
- Elastic bars: :
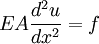
- Torsion of bars: :
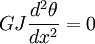
- Electrostatics: :
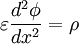
Problem 4: Least Squares Method
Given:
The residual over an element is
where
In the least squares approach, the residual is minimized in the following sense
Solution
Part 1
What is the weighting function used in the least squares approach?
We have,
Hence the weighting functions are of the form
Part 2
Develop a least-squares finite element model for the problem.
To make the typing of the following easier, I have gotten rid of the subscript 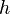 and the superscript
and the superscript  . Please note that these are implicit in what follows.
. Please note that these are implicit in what follows.
We start with the approximate solution
The residual is
The derivative of the residual is
For simplicity, let us assume that 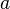 is constant, and
is constant, and 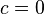 .
Then, we have
.
Then, we have
and
Now, the coefficients 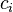 are independent. Hence, their derivatives
are
are independent. Hence, their derivatives
are
Hence, the weighting functions are
The product of these two quantities is
Therefore,
These equations can be written as
where
and
Part 3
- Discuss some functions
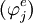 that can be used to approximate
that can be used to approximate 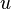
For the least squares method to be a true "finite element" type of method we have to use finite element shape functions. For instance, if each element has two nodes we could choose
Another possiblity is set set of polynomials such as
Problem 5: Heat Transefer
Given:
where 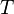 is the temperature,
is the temperature, 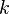 is the thermal conductivity, and
is the thermal conductivity, and
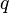 is the heat generation. The Boundary conditions are
is the heat generation. The Boundary conditions are
Solution
Part 1
Formulate the finite element model for this problem over one element
First step is to write the weighted-residual statement
Second step is to trade differentiation from 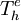 to
to 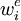 , using
integration by parts. We obtain
, using
integration by parts. We obtain
Rewriting (3) in using the primary variable 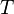 and
secondary variable
and
secondary variable 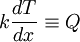 as described in the
text book to obtain the weak form
as described in the
text book to obtain the weak form
From (4) we have the following
Part 2
Use ANSYS to solve the problem of heat conduction in an insulated rod. Compare the solution with the exact solution. Try at least three refinements of the mesh to confirm that your solution converges.
The following inputs are used to solve for the solution of this problem:
/prep7
pi = 4*atan(1) !compute value for pi
ET,1,LINK34!convection element
ET,2,LINK32!conduction element
R,1,1!AREA = 1
MP,KXX,1,0.01!conductivity
MP,HF,1,25 !convectivity
emax = 2
length = 0.1
*do,nnumber,1,emax+1 !begin loop to creat nodes
n,nnumber,length/emax*(nnumber-1),0
n,emax+2,length,0!extra node for the convetion element
*enddo
type,2 !switch to conduction element
*do,enumber,1,emax
e,enumber,enumber+1
*enddo
TYPE,1 !switch to convection element
e,emax+1,emax+2!creat zero length element
D,1,TEMP,50
D,emax+2,TEMP,5
FINISH
/solu
solve
fini
/post1
/output,p5,txt
prnsol,temp
prnld,heat
/output,,
fini
ANSYS gives the following results
| Node | Temperature |
|---|---|
| 1 | 50.000 |
| 2 | 27.590 |
| 3 | 5.1793 |
| Node | Heat Flux |
|---|---|
| 1 | -4.4821 |
| 4 | 4.4821 |
Part 3
Write you own code to solve the problem in part 2.
The following Maple code can be used to solve the problem.
> restart;
> with(linalg):
> L:=0.1:kxx:=0.01:beta:=25:T0:=50:Tinf:=5:
> # Number of elements
> element:=10:
> # Division length
> ndiv:=L/element:
> # Define node location
> for i from 1 to element+1 do
> x[i]:=ndiv*(i-1);
> od:
> # Define shape function
> for j from 1 to element do
> N[j][1]:=(x[j+1]-x)/ndiv;
> N[j][2]:=(x-x[j])/ndiv;
> od:
> # Create element stiffness matrix
> for k from 1 to element do
> for i from 1 to 2 do
> for j from 1 to 2 do
> Kde[k][i,j]:=int(kxx*diff(N[k][i],x)*diff(N[k][j],x),x=x[k]..x[k+1]);
> od;
> od;
> od;
> Kde[0][2,2]:=0:Kde[element+1][1,1]:=0:
> # Create global matrix for conduction Kdg and convection Khg
> Kdg:=Matrix(1..element+1,1..element+1,shape=symmetric):
> Khg:=Matrix(1..element+1,1..element+1,shape=symmetric):
> for k from 1 to element+1 do
> Kdg[k,k]:=Kde[k-1][2,2]+Kde[k][1,1];
> if (k <= element) then
> Kdg[k,k+1]:=Kde[k][1,2];
> end if;
> od:
> Khg[element+1,element+1]:=beta:
> # Create global matrix Kg = Kdg + Khg
> Kg:=matadd(Kdg,Khg):
> # Create T and F vectors
> Tvect:=vector(element+1):Fvect:=vector(element+1):
> for i from 1 to element do
> Tvect[i+1]:=T[i+1]:
> Fvect[i]:=f[i]:
> od:
> Tvect[1]:=T0:
> Fvect[element+1]:=Tinf*beta:
> # Solve the system Ku=f
> Ku:=multiply(Kg,Tvect):
> # Create new K matrix without first row and column from Kg
> newK:=Matrix(1..element,1..element):
> for i from 1 to element do
> for j from 1 to element do
> newK[i,j]:=coeff(Ku[i+1],Tvect[j+1]);
> od;
> od;
> # Create new f matrix without f1
> newf:=vector(element,0):
> newf[1]:=-Ku[2]+coeff(Ku[2],T[2])*T[2]+coeff(Ku[2],T[3])*T[3]:
> newf[element]:=Tinf*beta:
> # Solve the system newK*T=newf
> solution:=multiply(inverse(newK),newf);
> exact := 50-448.2071713*x;
> with(plots):
> # Warning, the name changecoords has been redefined
> data := [[ x[n+1], solution[n]] <math>n=1..element]:
> FE:=plot(data, x=0..L, style=point,symbol=circle,legend="FE"):
> ELAS:=plot(exact,x=0..L,legend="exact",color=black):
> display({FE,ELAS},title="T(x) vs x",labels=["x","T(x)"]);
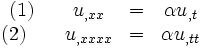

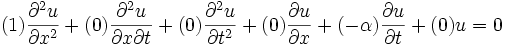
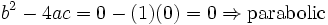
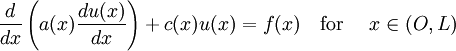
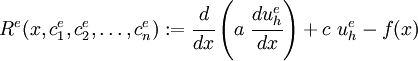
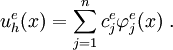
![\frac{\partial }{\partial c_i}\int_{x_a}^{x_b}
[R^e(x,c^e_1,c^e_2,\dots,c^e_n)]^2~dx = 0,
\qquad i=1,2,\dots,n ~.](../I/m/7de629d08aef872c89d3e2f67265129c.png)
![\frac{\partial }{\partial c_i}\int_{x_a}^{x_b} [R^e]^2~dx =
\int_{x_a}^{x_b} 2R^e\frac{\partial R^e}{\partial c_i}~dx = 0 ~.](../I/m/0b19adcc190a15beb2d6336f5a3c5cfd.png)
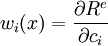
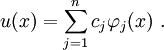
![R = \cfrac{d}{dx}\left[a~\left(\sum_j c_j\cfrac{d\varphi_j}{dx}\right)
\right] + c~\left(\sum_j c_j\varphi_j\right) - f(x) ~.](../I/m/3e27f579cee92159bd9d0dd2638dc8b0.png)
![\frac{\partial R}{\partial c_i} =
\cfrac{d}{dx}\left[a~\left(\sum_j \frac{\partial c_j}{\partial c_i}
\cfrac{d\varphi_j}{dx}\right)
\right] + c~\left(\sum_j \frac{\partial c_j}{\partial c_i}\varphi_j\right)
- f(x) ~.](../I/m/f737caa62752561b7fb9c2eecdbefe86.png)
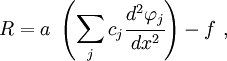
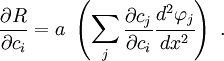
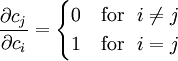
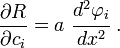
![R\frac{\partial R}{\partial c_i} =
\left(a\sum_j c_j\cfrac{d^2\varphi_j}{dx^2} - f\right)
\left(a\cfrac{d^2\varphi_i}{dx^2}\right) =
\sum_j \left[
\left(a^2\cfrac{d^2\varphi_i}{dx^2}\cfrac{d^2\varphi_j}{dx^2}\right)
c_j \right] - af\cfrac{d^2\varphi_i}{dx^2}~.](../I/m/f44336b3d4175dd94d0d1c8d06971d32.png)
![\int_{x_a}^{x_b} R\frac{\partial R}{\partial c_i}~dx = 0 \implies
\sum_j \left[
\left(\int_{x_a}^{x_b}
a^2\cfrac{d^2\varphi_i}{dx^2}\cfrac{d^2\varphi_j}{dx^2}~dx\right)
c_j \right] -
\int_{x_a}^{x_b} af\cfrac{d^2\varphi_i}{dx^2}~dx
= 0](../I/m/bc781f33c20fb775262698c32163f477.png)
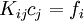
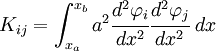
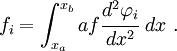
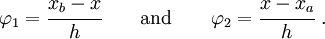
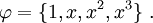
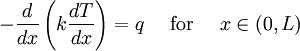
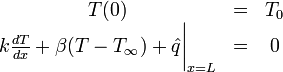
![0=\int_{x_a}^{x_b} w_i^e\left[-\frac{d}{dx}\left(
k\frac{dT_h^e}{dx}\right)-q\right]dx](../I/m/811a4354a2091ac8f263e333bce31716.png)
![0=\int_{x_a}^{x_b} \left(k\frac{w_i^e}{dx}\frac{dT_h^e}{dx}-
w_i^eq\right)dx-\left[w_i^ek\frac{dT_h^e}{dx}\right]_{x_a}^{x_b}
\text{(3)} \qquad](../I/m/aeac2ebd9ad33f86b00eb7de7ced74df.png)