Nonlinear finite elements/Homework 11/Solutions

< Nonlinear finite elements < Homework 11
Given:
For small strains, the strain tensor is given by
\boldsymbol{\varepsilon} = \frac{1}{2}\left[\boldsymbol{\nabla} \mathbf{u} + (\boldsymbol{\nabla} \mathbf{u})^T\right] \qquad\text{or}\qquad \varepsilon_{ij} = \frac{1}{2}(u_{i,j} + u_{j,i}) ~.
In classical (small strain) rate-independent plasticity we start off with an additive decomposition :of the strain tensor
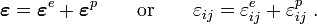
\boldsymbol{\varepsilon} = \boldsymbol{\varepsilon}^e + \boldsymbol{\varepsilon}^p \qquad\text{or}\qquad \varepsilon_{ij} = \varepsilon_{ij}^e + \varepsilon_{ij}^p ~.
Assuming linear elasticity, we have the following elastic stress-strain law
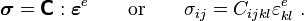
\boldsymbol{\sigma} = \boldsymbol{\mathsf{C}} : \boldsymbol{\varepsilon}^e \qquad\text{or}\qquad \sigma_{ij} = C_{ijkl}\varepsilon_{kl}^e ~.
Let us assume that the 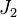J_2 theory applies during plastic deformation of the material. :Hence, the material obeys an associated flow rule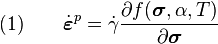
\text{(1)} \qquad \dot{\boldsymbol{\varepsilon}}^p = \dot{\gamma}\frac{\partial f(\boldsymbol{\sigma},\alpha,T)}{\partial \boldsymbol{\sigma}}
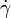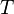where \dot{\gamma} is the plastic flow rate, f is the yield function, T is the temperature, and 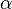\alpha is an internal variable.


This article is issued from Wikiversity - version of the Friday, January 18, 2008. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.