Nonlinear finite elements/Euler Bernoulli beams
< Nonlinear finite elementsEuler-Bernoulli Beam
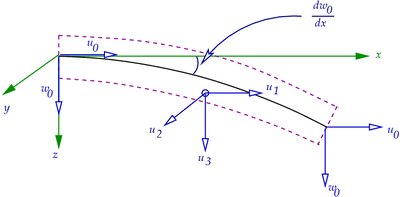 Euler-Bernoulli beam |
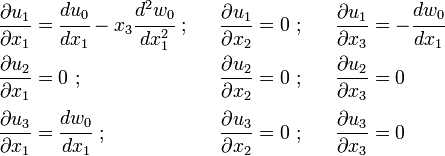
Displacements
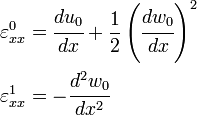
Strains
Strain-Displacement Relations
The displacements
The derivatives
von Karman strains
The von Karman strains
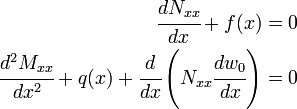
Equilibrium Equations
Balance of forces
Stress Resultants
Constitutive Relations
Stress-Strain equation
Stress Resultant - Displacement relations
Extensional/Bending Stiffness
If  is constant, and
is constant, and  -axis passes through centroid
-axis passes through centroid
Weak Forms
Axial Equation
where
Bending Equation
where
Finite Element Model
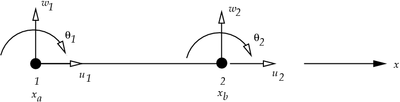 Finite element model for Euler Bernoulli beam |
where 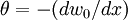 .
.
Hermite Cubic Shape Functions
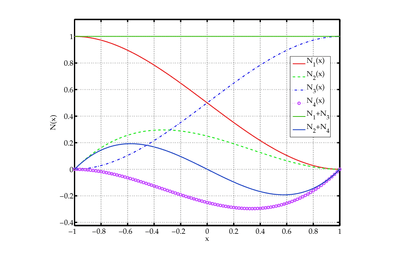 Hermite shape functions for beam |
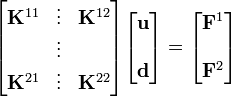
Finite Element Equations
where
Symmetric Stiffness Matrix
Load Vector
Newton-Raphson Solution
where
The residual is
For Newton iterations, we use the algorithm
where the tangent stiffness matrix is given by
Tangent Stiffness Matrix
Load Steps
Recall
- Divide load into small increments.
- Compute
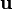 and
and 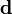 for first load step,
for first load step,
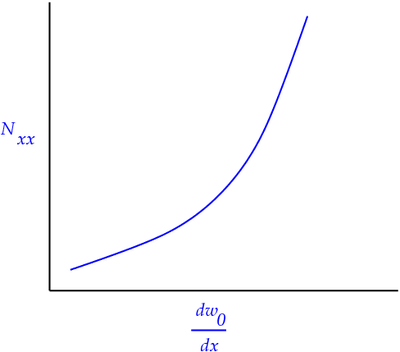 Stiffness of Euler-Bernoulli beam. |
- Compute
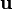 and
and 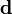 for second load step,
for second load step,
- Continue until F is reached.
Membrane Locking
Recall
where
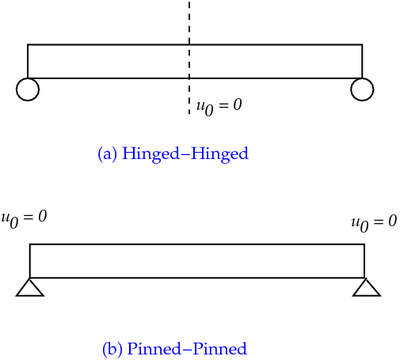 Mebrane locking in Euler-Bernoulli beam |
For Hinged-Hinged
Membrane strain:
or
Hence, shape functions should be such that
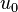 linear,
linear, 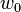 cubic
cubic  Element Locks!
Too stiff.
Element Locks!
Too stiff.
Selective Reduced Integration
- Assume
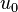 is linear ;~~
is linear ;~~ 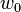 is cubic.
is cubic. - Then
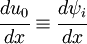 is constant, and
is constant, and 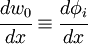 is quadratic.
is quadratic. - Try to keep
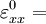 constant.
constant.
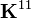 integrand is constant,
integrand is constant, 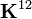 integrand is fourth-order ,
integrand is fourth-order , 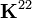 integrand is eighth-order
integrand is eighth-order
Full integration
Assume 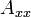 = constant.
= constant.
This article is issued from Wikiversity - version of the Tuesday, November 20, 2012. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.
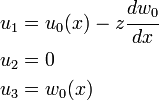
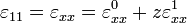
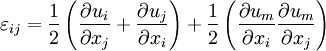
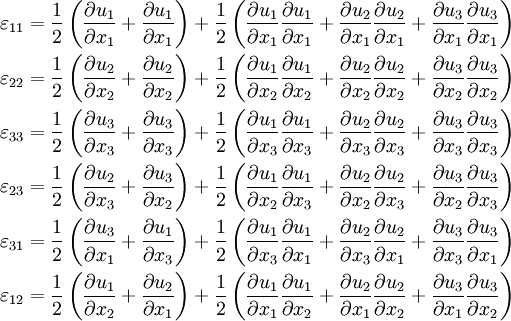
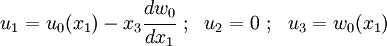
![\begin{align}
\varepsilon_{11} & = \cfrac{du_0}{dx_1} - x_3\cfrac{d^2w_0}{dx_1^2} +
\frac{1}{2}\left[
\left(\cfrac{du_0}{dx_1}-x_3\cfrac{d^2w_0}{dx_1^2}\right)^2 +
\left(\cfrac{dw_0}{dx_1}\right)^2\right] \\
\varepsilon_{22} & = 0 \\
\varepsilon_{33} & = \frac{1}{2}\left(\cfrac{dw_0}{dx_1}\right)^2 \\
\varepsilon_{23} & = 0 \\
\varepsilon_{31} & =
\frac{1}{2}\left(\cfrac{dw_0}{dx_1}-\cfrac{dw_0}{dx_1}\right) -
\frac{1}{2}\left[\left(\cfrac{du_0}{dx_1}-x_3\cfrac{d^2w_0}{dx_1^2}\right)
\left(\cfrac{dw_0}{dx_1}\right)\right] \\
\varepsilon_{12} & = 0
\end{align}](../I/m/a9bef33f65804141cd764b705d66a7e3.png)
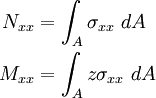
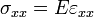
![\begin{align}
N_{xx} & = A_{xx} \varepsilon_{xx}^0 + B_{xx} \varepsilon_{xx}^1 =
A_{xx}\left[\cfrac{du_0}{dx} + \frac{1}{2}\left(\cfrac{dw_0}{dx}\right)^2 \right] -
B_{xx}\cfrac{d^2w_0}{dx^2} \\
M_{xx} & = B_{xx} \varepsilon_{xx}^0 + D_{xx} \varepsilon_{xx}^1 =
B_{xx}\left[\cfrac{du_0}{dx} + \frac{1}{2}\left(\cfrac{dw_0}{dx}\right)^2 \right] -
D_{xx}\cfrac{d^2w_0}{dx^2}
\end{align}](../I/m/cf3f7254c582670dcabfe121e9ac1791.png)

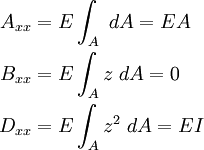
![\begin{align}
\int_{x_a}^{x_b} \cfrac{d(\delta u_0)}{dx}
\left[\cfrac{du_0}{dx} + \frac{1}{2}\left(\cfrac{dw_0}{dx}\right)^2\right]
A_{xx}~dx & =
\int_{x_a}^{x_b} (\delta u_0) f~dx +\\
& \delta u_0(x_a) Q_1 + \delta u_0(x_b) Q_4
\end{align}](../I/m/a0debfd31119041c47c8c8ddfc6bc40c.png)
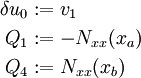
![\begin{align}
\int_{x_a}^{x_b} \left\{\cfrac{d(\delta w_0)}{dx} \right. &
\left[\cfrac{du_0}{dx} + \cfrac{1}{2}~\left(\cfrac{dw_0}{dx}\right)^2\right] \cfrac{dw_0}{dx} A_{xx} +
\left.\cfrac{d^2(\delta w_0)}{dx^2} \left(\cfrac{d^2w_0}{dx^2}\right) D_{xx} \right\}~dx= \\
& \int_{x_a}^{x_b} (\delta w_0) q~dx +
\delta w_0(x_a) Q_2 + \delta w_0(x_b) Q_5 +
\delta \theta(x_a) Q_3 +
\delta \theta(x_b) Q_6 ~.
\end{align}](../I/m/802cd0e03048512917f331c488123904.png)
![\begin{align}
\delta w_0 & := v_2 & \delta \theta & := \cfrac{dv_2}{dx} \\
Q_2 & := -\left[\cfrac{dM_{xx}}{dx} + N_{xx}\cfrac{dw_0}{dx}\right]_{x_a} &
Q_5 & := \left[\cfrac{dM_{xx}}{dx} + N_{xx}\cfrac{dw_0}{dx}\right]_{x_b} \\
Q_3 & := -M_{xx} (x_a) &
Q_6 & := M_{xx} (x_b)
\end{align}](../I/m/d9a5068daeb4f405f096a575fa54e6aa.png)
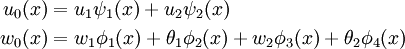
![\begin{align}
\mathbf{u} & = [u_1 \quad u_2]^T \\
\mathbf{d} & = [w_1 \quad \theta_1 \quad w_2 \quad \theta_2]^T
\end{align}](../I/m/43e8263bcc9fe19fe3a074b8dc8e7a67.png)

![\begin{align}
K_{ij}^{11} & = \int_{x_a}^{x_b} A_{xx}\cfrac{d\psi_i}{dx}\cfrac{d\psi_j}{dx}~dx \\
K_{ij}^{12} & = \frac{1}{2} \int_{x_a}^{x_b} \left(A_{xx}\cfrac{dw_0}{dx}\right)
\cfrac{d\psi_i}{dx} \cfrac{d\phi_j}{dx}~dx\\
K_{ij}^{21} & = \frac{1}{2} \int_{x_a}^{x_b} \left(A_{xx} \cfrac{dw_0}{dx}\right)
\cfrac{d\phi_i}{dx}\cfrac{d\psi_j}{dx}~dx\\
K_{ij}^{22} & = \int_{x_a}^{x_b}\left\{
\frac{1}{2} A_{xx}
\left[\cfrac{du_0}{dx}+\left(\cfrac{dw_0}{dx}\right)^2\right]
\cfrac{d\phi_i}{dx}\cfrac{d\phi_j}{dx} +
D_{xx}\cfrac{d^2\phi_i}{dx^2}\cfrac{d^2\phi_j}{dx^2}\right\}~dx
\end{align}](../I/m/dde16a18835793d1265342e5051b4806.png)
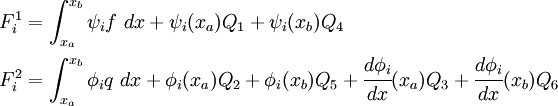
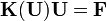
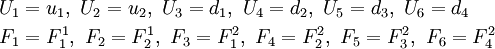
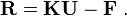
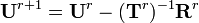
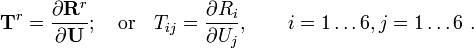
![\begin{align}
i=1\dots2;~j=1\dots2 &: \\
& { T^{11}_{ij} = K^{11}_{ij}} \\
\\
i=1\dots2;~j=1\dots4 &: \\
& { T^{12}_{ij} = 2 K^{12}_{ij}} \\
\\
i=1\dots4;~j=1\dots2 &: \\
& { T^{21}_{ij} = 2 K^{21}_{ij}} \\
\\
i=1\dots4;~j=1\dots4 &: \\
& { T^{22}_{ij} = K^{22}_{ij} +
\frac{1}{2} \int_{x_a}^{x_b} A_{xx}\left[\cfrac{du_0}{dx} +
2\left(\cfrac{dw_0}{dx}\right)^2\right]
\cfrac{d\phi_i}{dx}\cfrac{d\phi_j}{dx}~dx }
\end{align}](../I/m/2074d63c4b6782a8b410bcfabe206d9b.png)
![N_{xx} =
A_{xx}\left[\cfrac{du_0}{dx} + \frac{1}{2}\left(\cfrac{dw_0}{dx}\right)^2 \right] -
{{B_{xx}}}~~\cfrac{d^2w_0}{dx^2}](../I/m/841162d3776607638097496216a3d443.png)
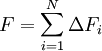
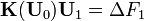
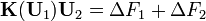
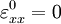
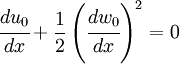
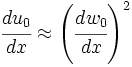
![\begin{align}
K_{ij}^{11} & = \int_{x_a}^{x_b} A_{xx}\cfrac{d\psi_i}{dx}\cfrac{d\psi_j}{dx}~dx\\
K_{ij}^{12} & = \frac{1}{2} \int_{x_a}^{x_b} \left(A_{xx}\cfrac{dw_0}{dx}\right) \cfrac{d\psi_i}{dx} \cfrac{d\phi_j}{dx}~dx\\
K_{ij}^{22} & = \int_{x_a}^{x_b}\left\{\frac{1}{2} A_{xx} \left[\cfrac{du_0}{dx}+\left(\cfrac{dw_0}{dx}\right)^2\right] \cfrac{d\phi_i}{dx}\cfrac{d\phi_j}{dx} + D_{xx}\cfrac{d^2\phi_i}{dx^2}\cfrac{d^2\phi_j}{dx^2}\right\}~dx
\end{align}](../I/m/7cadab54a0347e4052d8ae4ec734e996.png)
![n_{\text{gauss pt}} = \text{int}[(p+1)/2] + 1](../I/m/19f03fbda95639f4abac3fb86c1c43c7.png)
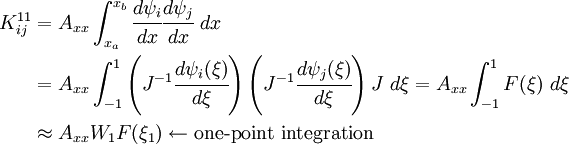
![\begin{align}
K_{ij}^{12} & = \frac{1}{2} \int_{x_a}^{x_b} \left(A_{xx}\cfrac{dw_0}{dx}\right)
\cfrac{d\psi_i}{dx} \cfrac{d\phi_j}{dx}~dx\\
& = \cfrac{A_{xx}}{2} \int_{-1}^{1}
\left(\sum_{i=1}^4 w_i J^{-1}\cfrac{d\phi_i(\xi)}{d\xi}\right)
\left(J^{-1}\cfrac{d\psi_i(\xi)}{d\xi}\right)
\left(J^{-1}\cfrac{d\phi_j(\xi)}{d\xi}\right)~dx \\
& \approx A_{xx}\left[ W_1 F(\xi_1) + W_2 F(\xi_2) + W_3 F(\xi_3)\right]
\leftarrow { \text{full integration}} \\
& \approx A_{xx}\left[ W_1 F(\xi_1) + W_2 F(\xi_2)\right]
\leftarrow { \text{reduced integration}}
\end{align}](../I/m/aacdc123273df5504b4bed6a756527ed.png)