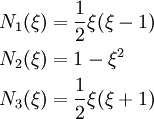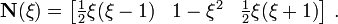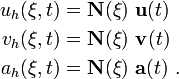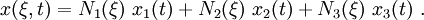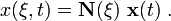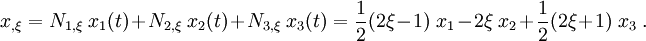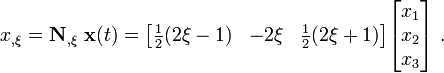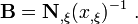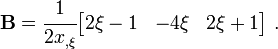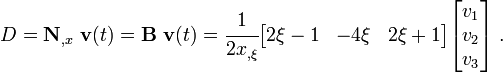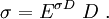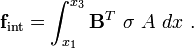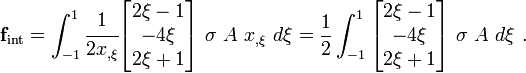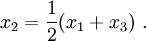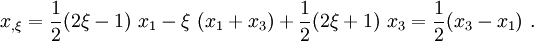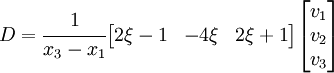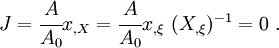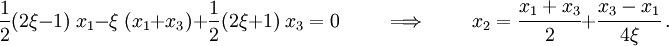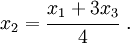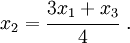Nonlinear finite elements/Effect of mesh distortion
< Nonlinear finite elementsAn Example: Effect of Mesh Distortion
Consider the three-noded quadratic displacement element shown in Figure 1.
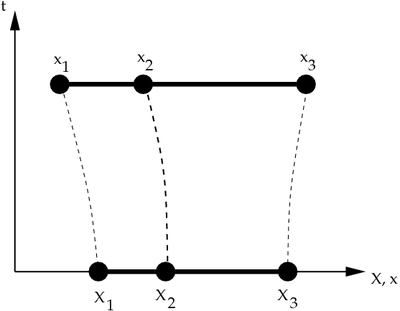 Figure 1. Reference and Current Configurations of a 3-noded element. |
The shape functions for the parent element are
In matrix form,
The trial functions (in terms of the parent coordinates) are
The mapping from the Eulerian coordinates to the parent element coordinates is
In matrix form,
Therefore, the derivative with respect to 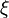 is
is
In matrix form,
Now, the 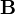 matrix is given by
matrix is given by
Therefore,
The rate of deformation is then given by
The stress can be calculated using the relation
The internal forces are given by
Plugging in the expression for 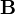 , and changing the limits of
integration, we get
, and changing the limits of
integration, we get
If node 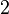 is midway between node
is midway between node 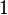 and node
and node 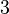 ,
,
Then we have,
The rate of deformation becomes
which is a linear function of 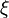 .
.
However, if node 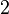 moves away from the middle during deformation, then
moves away from the middle during deformation, then
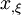 is no longer constant and can become zero or negative.
Under such situations the rate of deformation is either infinite or the
element inverts upon itself since the isoparametric map is no longer
one-to-one.
is no longer constant and can become zero or negative.
Under such situations the rate of deformation is either infinite or the
element inverts upon itself since the isoparametric map is no longer
one-to-one.
Let us consider the case where 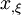 is zero. In that case,
the Jacobian becomes
is zero. In that case,
the Jacobian becomes
Similarly, when 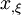 is negative,
is negative, 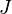 is negative. This implies that the conservation of mass is violated.
is negative. This implies that the conservation of mass is violated.
To find the location of 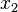 when this happens, we set the relation
for
when this happens, we set the relation
for 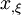 to zero. Then we get,
to zero. Then we get,
If 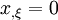 at
at 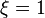 , then
, then
This means that as node 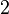 gets closer and closer to node
gets closer and closer to node 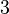 , the rate of
deformation become infinite at node
, the rate of
deformation become infinite at node 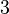 and then negative.
and then negative.
If 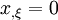 at
at 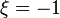 , then
, then
This means that as node 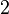 gets closer and closer to node
gets closer and closer to node 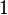 , the rate of
deformation becomes infinite at node
, the rate of
deformation becomes infinite at node 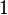 and then negative.
and then negative.
These effects of mesh distortion can be severe in multiple dimensions. That is the reason that linear elements are preferred in large deformation simulations.