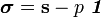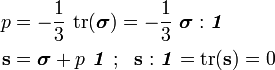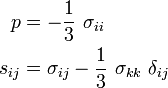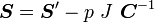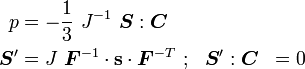Nonlinear finite elements/Deviatoric and volumetric stress

Deviatoric and volumetric stress

Often it is convenient to decompose the stress tensor into volumetric and deviatoric (distortional) parts. Applications of such decompositions can be found in metal plasticity, soil mechanics, and biomechanics.

Decomposition of the Cauchy stress

The Cauchy stress can be additively decomposed as

\boldsymbol{\sigma} = \mathbf{s} - p~\boldsymbol{\mathit{1}}

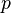where $\mathbf{s}$ is the deviatoric stress and $p$ is the pressure and

\begin{align} p & = - \frac{1}{3}~\text{tr}(\boldsymbol{\sigma}) = -\frac{1}{3}~\boldsymbol{\sigma}:\boldsymbol{\mathit{1}} \\ \mathbf{s} & = \boldsymbol{\sigma} + p~\boldsymbol{\mathit{1}} ~;~~ \mathbf{s}:\boldsymbol{\mathit{1}} = \text{tr}(\mathbf{s}) = 0 \end{align}

In index notation,

\begin{align} p & = -\frac{1}{3}~\sigma_{ii} \\ s_{ij} & = \sigma_{ij} - \frac{1}{3}~\sigma_{kk}~\delta_{ij} \end{align}

Decomposition of the 2nd P-K stress

The second Piola-Kirchhoff stress can be decomposed into volumetric and distortional parts as

\boldsymbol{S} = \boldsymbol{S}' - p~J~\boldsymbol{C}^{-1}

where

\begin{align} p & = -\frac{1}{3}~J^{-1}~\boldsymbol{S}:\boldsymbol{C} \\ \boldsymbol{S}' & = J~\boldsymbol{F}^{-1}\cdot\mathbf{s}\cdot\boldsymbol{F}^{-T} ~;~~ \boldsymbol{S}':\boldsymbol{C} & = 0 \end{align}

This article is issued from Wikiversity - version of the Saturday, September 12, 2009. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.