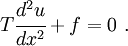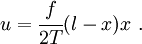Nonlinear finite elements/Calculus of variations
< Nonlinear finite elementsIdeas from the calculus of variations are commonly found in papers dealing with the finite element method. This handout discusses some of the basic notations and concepts of variational calculus. Most of the examples are from Variational Methods in Mechanics by T. Mura and T. Koya, Oxford University Press, 1992.
The calculus of variations is a sort of generalization of the calculus that you all know. The goal of variational calculus is to find the curve or surface that minimizes a given function. This function is usually a function of other functions and is also called a functional.
Maxima and minima of functions
The calculus of variations extends the ideas of maxima and minima of functions to functionals.
For a function of one variable  , the minimum occurs at some point
, the minimum occurs at some point  . For a functional, instead of a point minimum, we think in terms of a function that minimizes the functional. Thus, for a functional
. For a functional, instead of a point minimum, we think in terms of a function that minimizes the functional. Thus, for a functional ![I[f(x)]](../I/m/8a2e681dc71dbb4a464909b02b0f1dc1.png) we can have a minimizing function
we can have a minimizing function 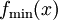 .
.
The problem of finding extrema (minima and maxima) or points of inflection (saddle points) can either be constrained or unconstrained.
The unconstrained problem.
Suppose 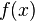 is a function of one variable. We want to find the maxima, minima, and points of inflection for this function. No additional constraints are imposed on the function. Then, from elementary calculus, the function
is a function of one variable. We want to find the maxima, minima, and points of inflection for this function. No additional constraints are imposed on the function. Then, from elementary calculus, the function 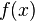 has
has
- a minimum if
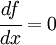 and
and 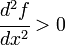 .
. - a maximum if
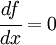 and
and 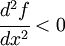 .
. - a point of inflection if
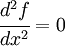 .
.
Any point where the condition 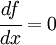 is satisfied is called a stationary point and we say that the function is stationary at that point.
is satisfied is called a stationary point and we say that the function is stationary at that point.
A similar concept is used when the function is of the form 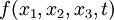 . Then, the function
. Then, the function 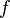 is stationary if
is stationary if
Since 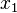 ,
, 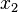 ,
, 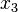 , and
, and 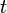 are independent variables, we can write the stationarity condition as
are independent variables, we can write the stationarity condition as
The constrained problem - Lagrange multipliers.
Suppose we have a function 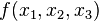 . We want to find the minimum (or maximum) of the function
. We want to find the minimum (or maximum) of the function 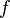 with the added constraint that
with the added constraint that
The added constraint is equivalent to saying that the variables 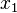 ,
, 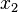 , and
, and 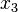 are not independent and we can write one of the variables in terms of the other two.
are not independent and we can write one of the variables in terms of the other two.
The stationarity condition for 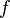 is
is
Since the variables 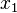 ,
, 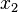 , and
, and 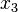 are not independent, the
coefficients of
are not independent, the
coefficients of 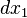 ,
, 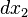 , and
, and 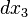 are not zero.
are not zero.
At this stage we could express 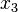 in terms of
in terms of 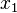 and
and 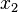 using the constraint equation (1), form another stationarity condition involving only
using the constraint equation (1), form another stationarity condition involving only 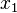 and
and 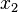 , and set the coefficients of
, and set the coefficients of 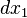 and
and 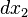 to zero. However, it is usually impossible to solve equation (1) analytically for
to zero. However, it is usually impossible to solve equation (1) analytically for 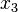 . Hence, we use a more convenient approach called the Lagrange multiplier method.
. Hence, we use a more convenient approach called the Lagrange multiplier method.
Lagrange multiplier method.
From equation (1) we have
We introduce a parameter 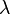 called the Lagrange multiplier and using equation (2) we get
called the Lagrange multiplier and using equation (2) we get
Then we have,
We choose the parameter 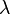 such that
such that
Then, because 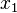 and
and 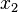 are independent, we must have
are independent, we must have
We can now use equations (1), (3), and (4) to solve for the extremum point and the Lagrange multiplier. The constraint is satisfied in the process.
Notice that equations (1), (3) and (4) can also be written as
where
Minima of functionals
Consider the functional
We wish to minimize the functional 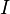 with the constraints (prescribed boundary conditions)
with the constraints (prescribed boundary conditions)
Let the function 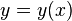 minimize
minimize 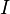 . Let us also choose a trial function (that is not quite equal to the solution
. Let us also choose a trial function (that is not quite equal to the solution 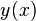 )
)
where 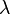 is a parameter, and
is a parameter, and 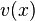 is an arbitrary continuous function that has the property that
is an arbitrary continuous function that has the property that
(See Figure 1 for a geometric interpretation.)
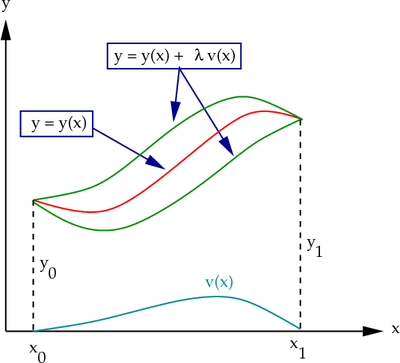 Figure 1. Minimizing function 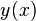 and trial functions. and trial functions. |
Plug (6) into (5) to get
You can show that equation (8) can be written as (show this)
where
and
The quantity 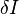 is called the first variation of
is called the first variation of 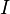 and
the quantity
and
the quantity 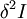 is called the second variation of
is called the second variation of 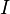 . Notice
that
. Notice
that 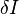 consists only of terms containing
consists only of terms containing 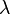 while
while
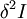 consists only of terms containing
consists only of terms containing 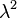 .
.
The necessary condition for ![I[y(x)]](../I/m/8163f118a753b1a62eabe8c2f6b1093a.png) to be a minimum is
to be a minimum is
Remark.
The first variation of the functional ![I[y]](../I/m/15ed8cca5742103c5bdb7f8e11f0dfb1.png) in the direction
in the direction 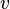 is defined as
is defined as
To find which function makes 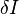 zero, we first integrate the first term of equation (9) by parts. We have,
zero, we first integrate the first term of equation (9) by parts. We have,
Since 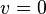 at
at 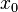 and
and 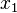 , we have
, we have
Plugging equation (12) into (9) and applying the minimizing condition (11), we get
or,
The fundamental lemma of variational calculus states that if 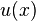 is a piecewise continuous function of
is a piecewise continuous function of 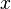 and
and 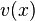 is a continuous function that vanishes on the boundary, then
is a continuous function that vanishes on the boundary, then
Applying (14) to (13) we get
Equation (15) is called the Euler equation of the functional 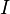 . The solution of the Euler equation is the minimizing function that we seek.
. The solution of the Euler equation is the minimizing function that we seek.
Of course, we cannot be sure that the solution represents and minimum unless we check the second variation 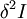 . From equation (10) we can see that
. From equation (10) we can see that 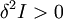 if
if 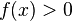 and
and 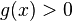 and in that case the problem is guaranteed to be a minimization problem.
and in that case the problem is guaranteed to be a minimization problem.
We often define
where 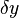 is called a variation of
is called a variation of 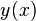 .
.
In this notation, equation (9) can be written as
You see this notation in the principle of virtual work in the mechanics of materials.
An example
Consider the string of length 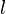 under a tension
under a tension 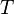 (see Figure 2). When a vertical load
(see Figure 2). When a vertical load 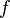 is applied, the string deforms by an amount
is applied, the string deforms by an amount 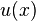 in the
in the 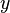 -direction. The deformed length of an element
-direction. The deformed length of an element 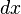 of the string is
of the string is
If the deformation is small, we can expand the relation into a Taylor series and ignore the higher order terms to get
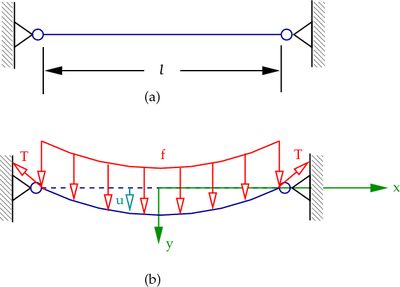 Figure 2. An elastic string under a transverse load. |
The force T in the string moves a distance
Therefore, the work done by the force 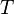 (per unit original length of the string) (the stored elastic energy) is
(per unit original length of the string) (the stored elastic energy) is
The work done by the forces 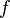 (per unit original length of string) is
(per unit original length of string) is
We want to minimize the total energy. Therefore, the functional to be minimized is
The Euler equation is
The solution is
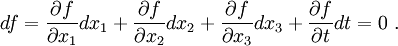
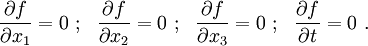
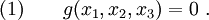
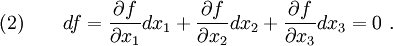
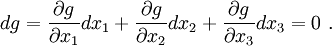
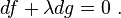
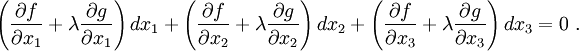
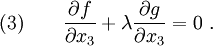
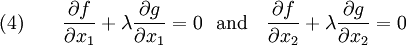
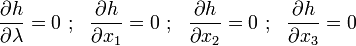
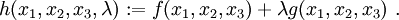
![\text{(5)} \qquad
I[y(x)] = \int_{x_0}^{x_1} \left[f(x)\left(\cfrac{dy(x)}{dx}\right)^2 +
g(x)y(x)^2 + 2h(x)y(x)\right] ~dx~.](../I/m/330541b26bf73295d3242297c1f8c7bf.png)

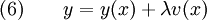
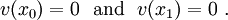
![\text{(8)} \qquad
I[y(x)+\lambda v(x)] =
\int_{x_0}^{x_1} \left[f(x)\left(\cfrac{dy(x)}{dx}+
\lambda\cfrac{dv}{dx}\right)^2 +
g(x)\left[y(x) + \lambda v(x)\right]^2 +
2h(x)\left[y(x) + \lambda v(x)\right]\right] ~dx~.](../I/m/31ab3516873b0da75ecbee7b71a3cfbc.png)
![I[y(x)+\lambda v(x)] = I[y(x)] + \delta I + \delta^2 I
~~~~\text{or,}~~~~
I[y(x)+\lambda v(x)] - I[y(x)] = \delta I + \delta^2 I](../I/m/833348a75e8d4e9e5ed3885d2bab8ab5.png)
![\text{(9)} \qquad
\delta I = 2\lambda \int_{x_0}^{x_1} \left[f(x)
\left(\cfrac{dy(x)}{dx}\right)
\left(\cfrac{dv(x)}{dx}\right) + g(x) y(x) v(x) + h(x) v(x)\right]~dx](../I/m/ba1817ebc25c8a380bf5ccf5832007ed.png)
![\text{(10)} \qquad
\delta^2 I = \lambda^2 \int_{x_0}^{x_1}
\left[f(x)\left(\cfrac{dv(x)}{dx}\right)^2 + g(x)[v(x)]^2\right]~dx~.](../I/m/84127a46167fa870ddbb36c9d207548f.png)
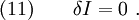
![{
\delta I(y;v) = \lim_{\epsilon\rightarrow 0}
\cfrac{I[y + \epsilon v] - I[y]}{\epsilon}
\equiv \left.\cfrac{d}{d\epsilon} I[y + \epsilon v]\right|_{\epsilon = 0}
~.}](../I/m/377984b80d2f3d39b9b95cb83dbdbd03.png)
![\int_{x_0}^{x_1} \left(f \cfrac{dy}{dx}\right)
\cfrac{dv}{dx}~dx =
\left[\left(f \cfrac{dy}{dx}\right) v \right]_{x_0}^{x_1} -
\int_{x_0}^{x_1} \cfrac{d}{dx}\left(f \cfrac{dy}{dx}\right) v~dx~.](../I/m/a1c614a108f2812b4b525389a223021e.png)
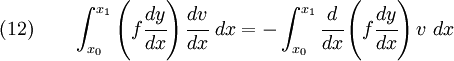
![0 = \int_{x_0}^{x_1} \left[-\cfrac{d}{dx}\left(f(x)
\cfrac{dy(x)}{dx}\right) v(x) +
g(x) y(x) v(x) + h(x) v(x)\right]~dx](../I/m/7ae2fd2a9a4f9d4f988e1efb7297e013.png)
![\text{(13)} \qquad
\int_{x_0}^{x_1} \left[-\cfrac{d}{dx}\left(f(x)
\cfrac{dy(x)}{dx}\right) +
g(x) y(x) + h(x) \right]v(x)~dx = 0~.](../I/m/d70a92cd65761b7fddfb294cba4237fe.png)
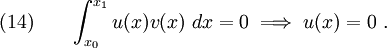
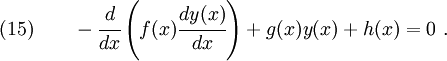
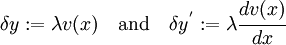
![\delta I = 2\int_{x_0}^{x_1}\left[f\left(\cfrac{dy}{dx}\right)\delta y^{'}
+ g y \delta y + h \delta y\right]~dx](../I/m/23e4c2a378a3421424ca9f82d0ea4d95.png)
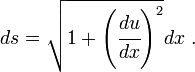
![ds = \left[1 + \frac{1}{2}\left(\cfrac{du}{dx}\right)^2\right] dx ~.](../I/m/e8bd832c291245d88fe3f4da0ee3aad1.png)
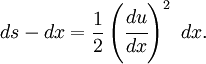
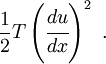
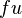
![I[y] = \cfrac{T}{2} \int_0^l \left(\cfrac{du}{dx}\right)^2~dx
- \int_0^l f u~dx ~.](../I/m/6c9fe0f5666dd339742a02c3ab1e3ae3.png)