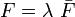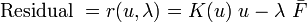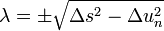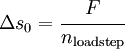Nonlinear finite elements/Buckling of beams

< Nonlinear finite elements

Nonlinear Post-Buckling

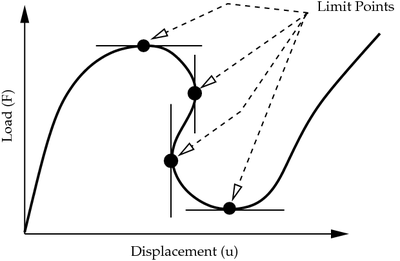Buckling of beams.

Newton-Raphson

Standard Newton-Raphon methods perform poorly for bucking problems.

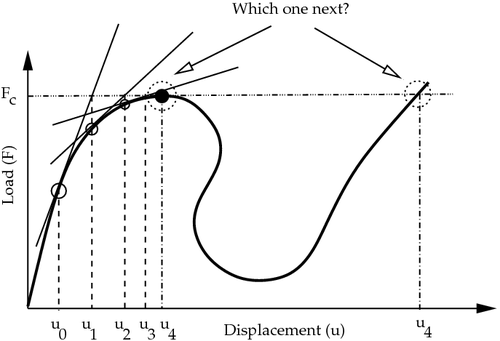Predicting buckling with Newton_Raphson.

Arc Length Method

Also called Modified Riks Method.
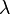Control the size of the load step using a parameter $\lambda$ .
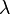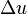Solve for both $\lambda$ and $\Delta u$ in each Newton iteration.

Assume 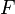$F$ = independent of geometry. Then

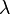F = \lambda~\bar{F}

$\lambda$ can be thought of as a normalized load parameter.

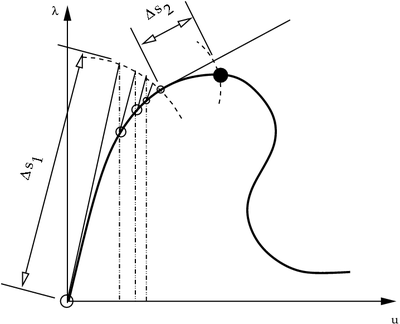\text{Residual}~= r(u, \lambda) = K(u)~u - \lambda~\bar{F}

Arc-length method

The load increment is computed using

\lambda = \pm\sqrt{\Delta s^2 - \Delta u_n^2}

The reference arc length

\Delta s_0 = \cfrac{F}{n_{\text{loadstep}}}

This article is issued from Wikiversity - version of the Wednesday, August 22, 2007. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.